Lab 7: Model evaluation

Not graded, just practice

1 Model accuracy

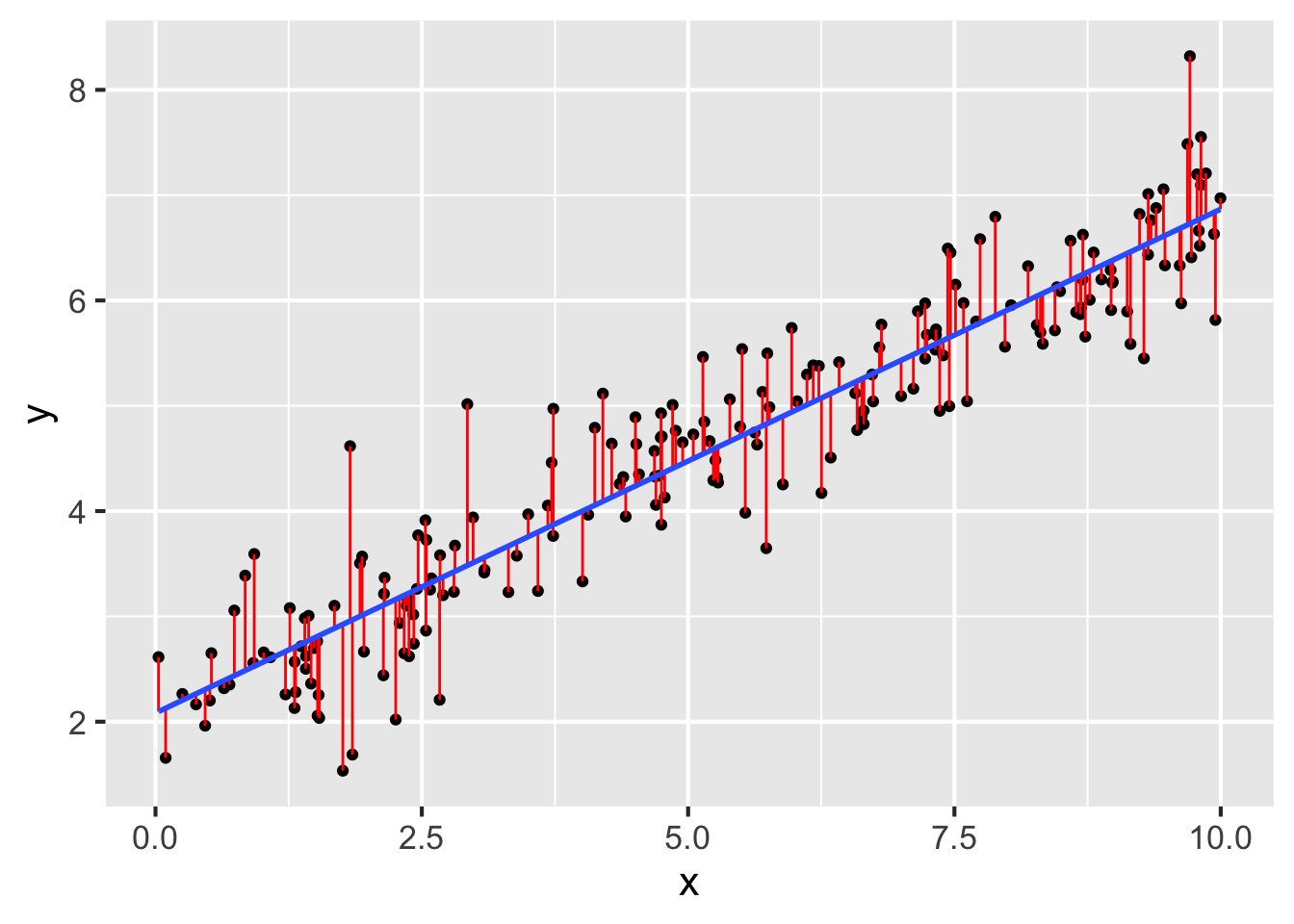
Question 13 refers to the following figure:

13. In the figure above, which of the following corresponds to the residuals?

blue line red lines black dots none of the above

14. Suppose the \(R^2\) value on the model in the figure above is about 0.88. Given this value, which of the following best describes the accuracy of the model?

fairly high accuracy fairly low accuracy not enough information

15. Suppose 0.88 reflects the \(R^2\) for our fitted model on our sample. Which of the following is true about the \(R^2\) for our fitted model on the population?

tends to be higher tends to be lower the same

16. Which of the following best describes an overfit model?

performs well predicting new values, but poorly on the sample performs well on the sample, but poorly predicting new values performs poorly both on the sample and predicting new values performs well both on the sample and predicting new values

17. How can we estimate \(R^2\) on the population? Choose all that apply.

cross validation bootstrapping set.seed none of the above

18. Fill in the blanks below to best describe cross validation:
    • Leave some out
    • Fit a model on the data left outkept in
    • Evaluate the mdoel on the data left outkept in

2 Model accuracy in R

Questions 19-20 refer to the following code and output:

model <- lm(y ~ 1 + x, data)
summary(model)

Call:
lm(formula = y ~ 1 + x, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.38959 -0.32626 -0.04605  0.31967  1.65977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.08280    0.07418   28.08   <2e-16 ***
x            0.47844    0.01242   38.51   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5139 on 198 degrees of freedom
Multiple R-squared:  0.8822,    Adjusted R-squared:  0.8816 
F-statistic:  1483 on 1 and 198 DF,  p-value: < 2.2e-16

19. What is the \(R^2\) value for the model fit above?

20. Does the value you entered in 19 reflect \(R^2\) on the population or on the sample?

population sample

Questions 21-23 refer to the following code and output:

# we divide the data into v folds for cross-validation
set.seed(2) 
splits <- vfold_cv(data)

# model secification 
model_spec <- 
  linear_reg() %>%  
  set_engine(engine = "lm")  

# add a workflow
our_workflow <- 
  workflow() %>%
  add_model(model_spec) %>%  
  add_formula(y ~ x) 

# fit models to our folds 
fitted_models <- 
  fit_resamples(
    object = our_workflow, 
    resamples = splits
    ) 

fitted_models %>%
    collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config        
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>          
1 rmse    standard   0.507    10  0.0397 pre0_mod0_post0
2 rsq     standard   0.890    10  0.0146 pre0_mod0_post0

21. In the cross-validation performed above, how many folds were the data split into?

2 5 10

22. What \(R^2\) do we estimate for the population?

23. What model has been fit?

y ~ x y ~ x^2 x ~ y vfold_cv

Questions 24-26 refer to the following code and output:

# we bootstrap the data for cross-validation
set.seed(2) 
bootstrap <- bootstraps(data) 

# fit models to our folds 
fitted_models_boot <- 
  fit_resamples(
    object = our_workflow, 
    resamples = bootstrap
    ) 

fitted_models_boot %>%
    collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config        
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>          
1 rmse    standard   0.507    25 0.00946 pre0_mod0_post0
2 rsq     standard   0.887    25 0.00377 pre0_mod0_post0

24. How many bootstrap samples did we generate?

25. True or false, we fit the same model to the bootstrap data as we did in the cross-validation code.

TRUE FALSE

26. True or false, the \(R^2\) estimated by bootstrapping is equal to the \(R^2\) estimated by cross-validation.

TRUE FALSE

3 Model reliability

1. As we collect more data, our parameter estimates

become more reliable become less reliable stay the same

2. Each figure below plots 100 bootstrapped models with data drawn from the same population. In one figure, the model is fit to 10 data points. In the other, each model is fit to 200 data points. Which figure shows the model fit to 200 data points?

Figure A Figure B Both figures have the same number of data points

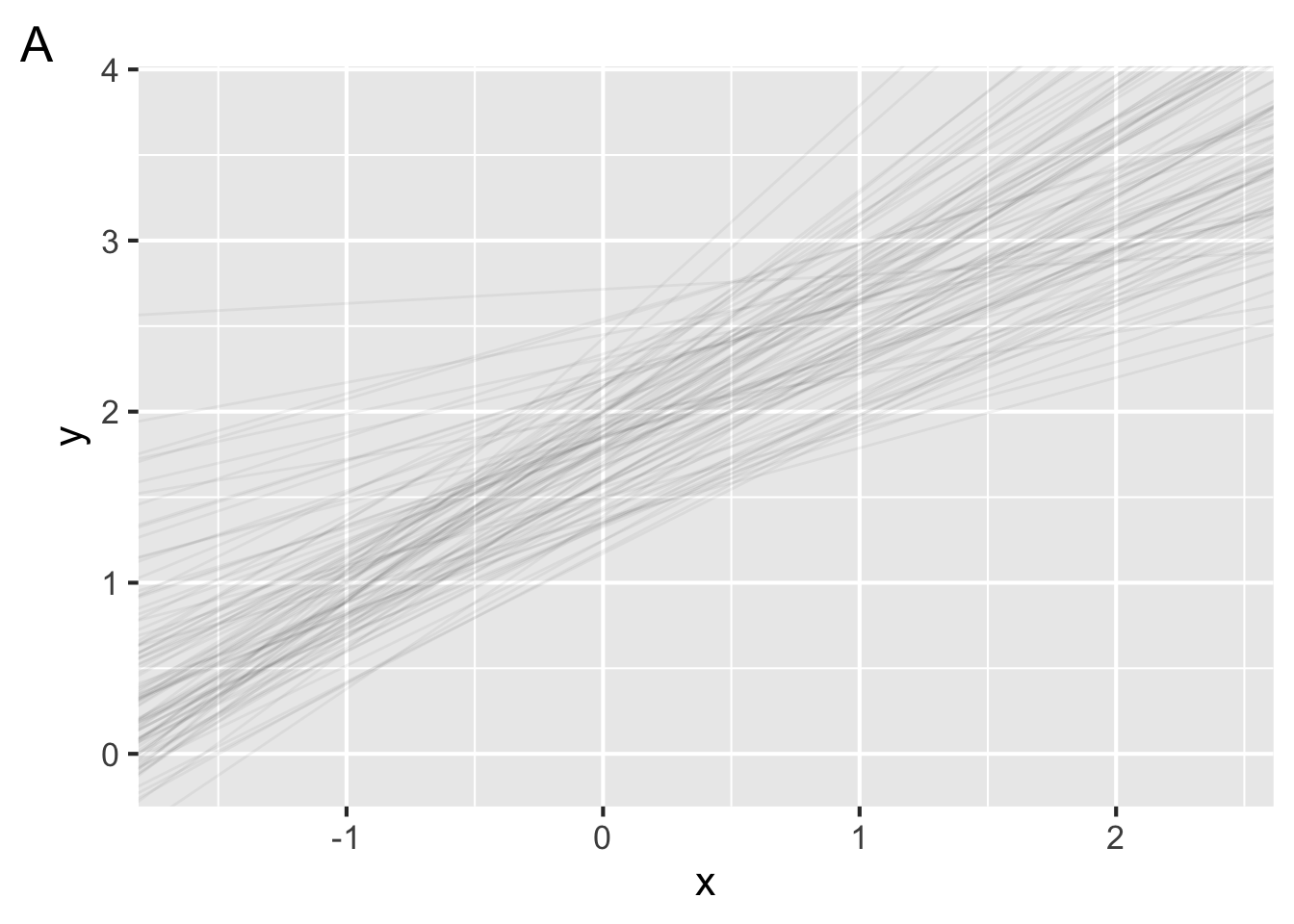
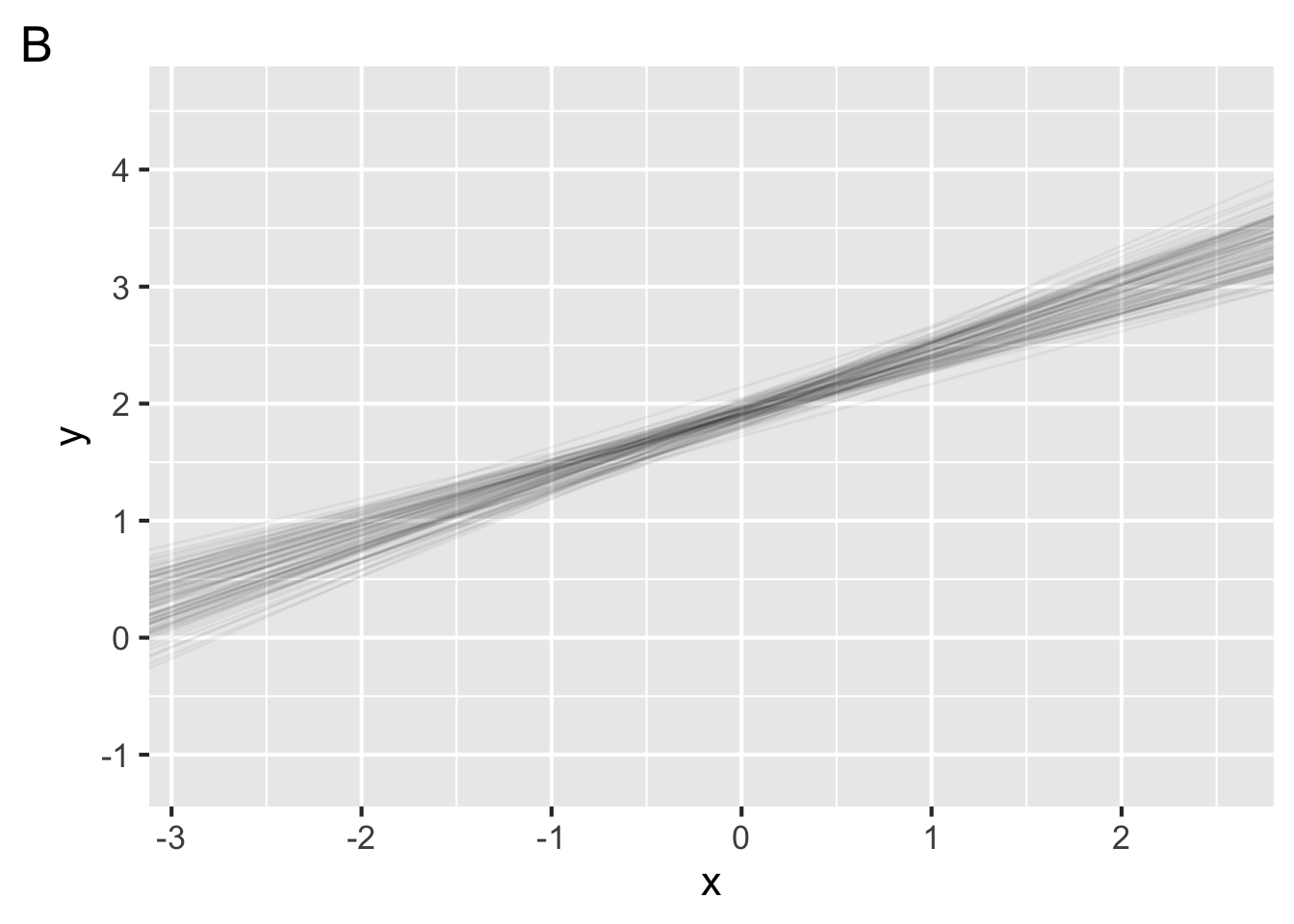
3. As we collect more data, what happens to the confidence interval around our parameter estimates?

It gets bigger (wider) It stays the same It gets smaller (narrower)

4. True or false, we can obtain confidence intervals around parameter estimates for models in the same we we did for point estimates like the mean.

True False

5. Model reliability asks how certain we can be about our parameter estimates. Why is there uncertainty around our parameter estimates?

"Because we are interested in the model parameters that 
best describe the population from which the sample was
 drawn. Due to sampling error, we can expect some 
 variability in the model parameters."

6. The figure below shows the model fit for a sample of 10 participants. Suppose we repeated our experiment with 10 new participants. True or false, fitting the same model to these new data would yield approximately the same parameter estimates.

True False

7. True or false, a model with high accuracy must also have high reliability.

True False