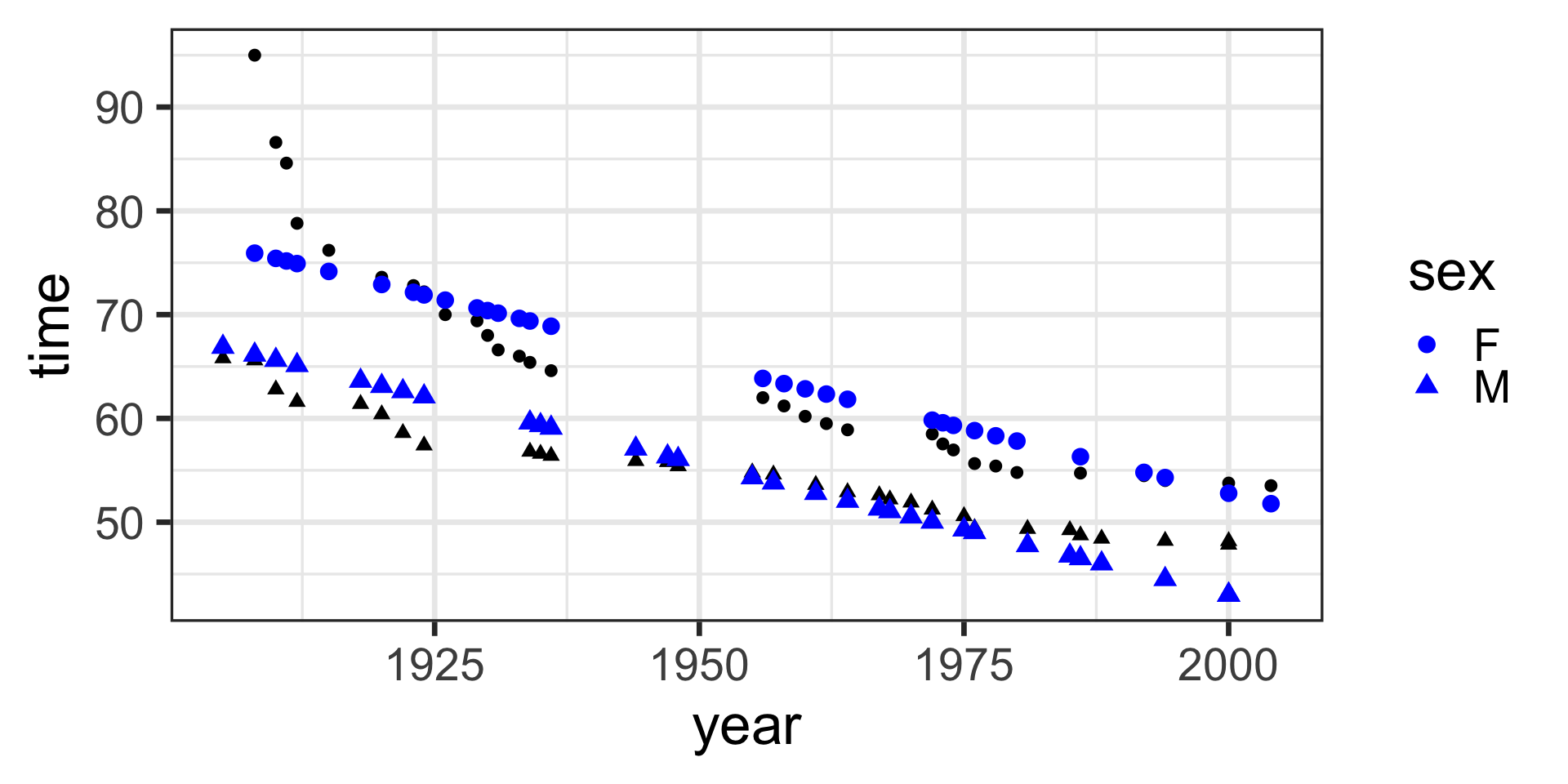
Main
- in R:
y ~ 1 + year, in eq: \(y = w_1x_1 + w_2x_2\)
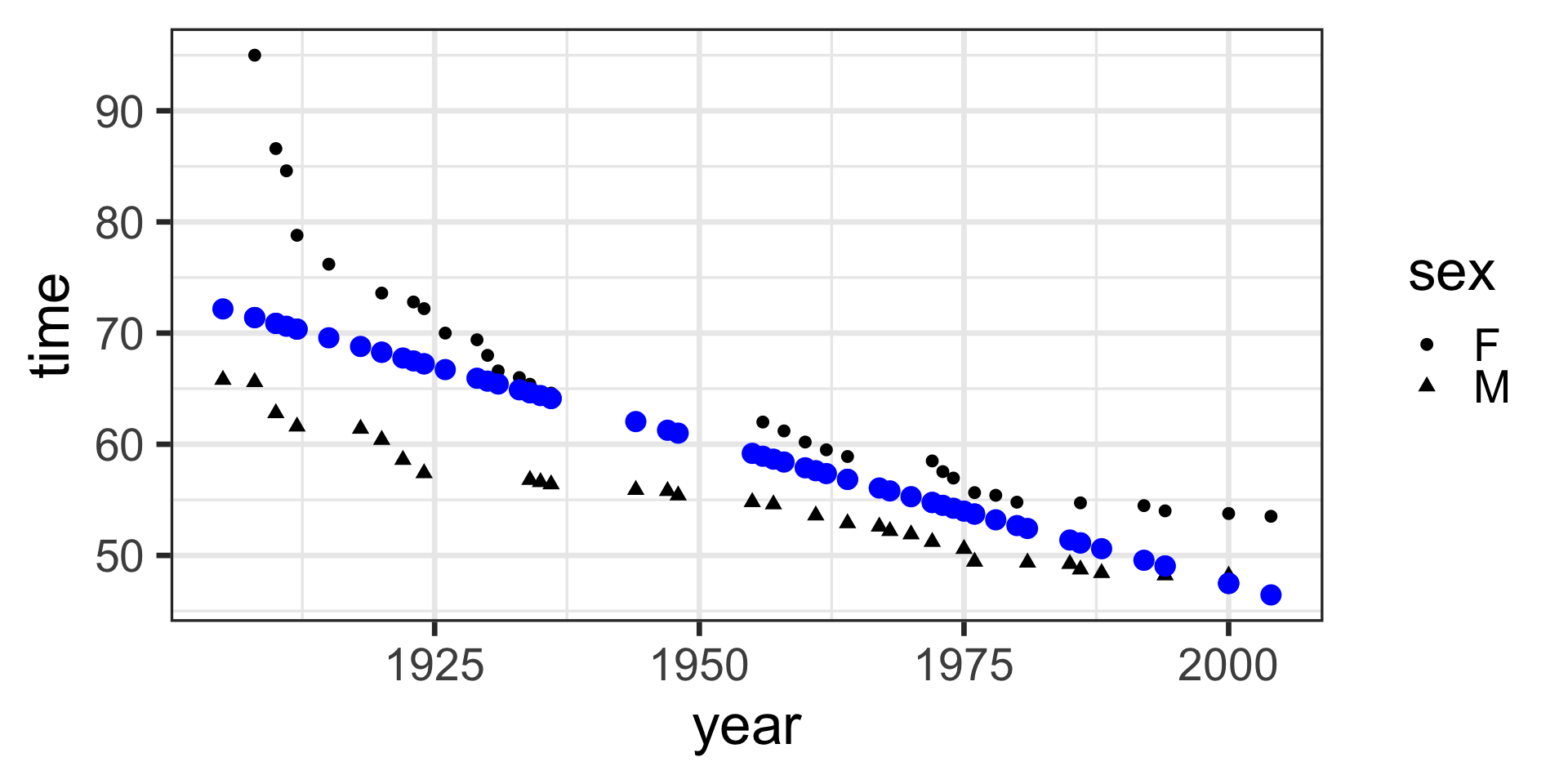
- in R:
y ~ 1 + sex, in eq: \(y = w_1x_1 + w_2x_2\)
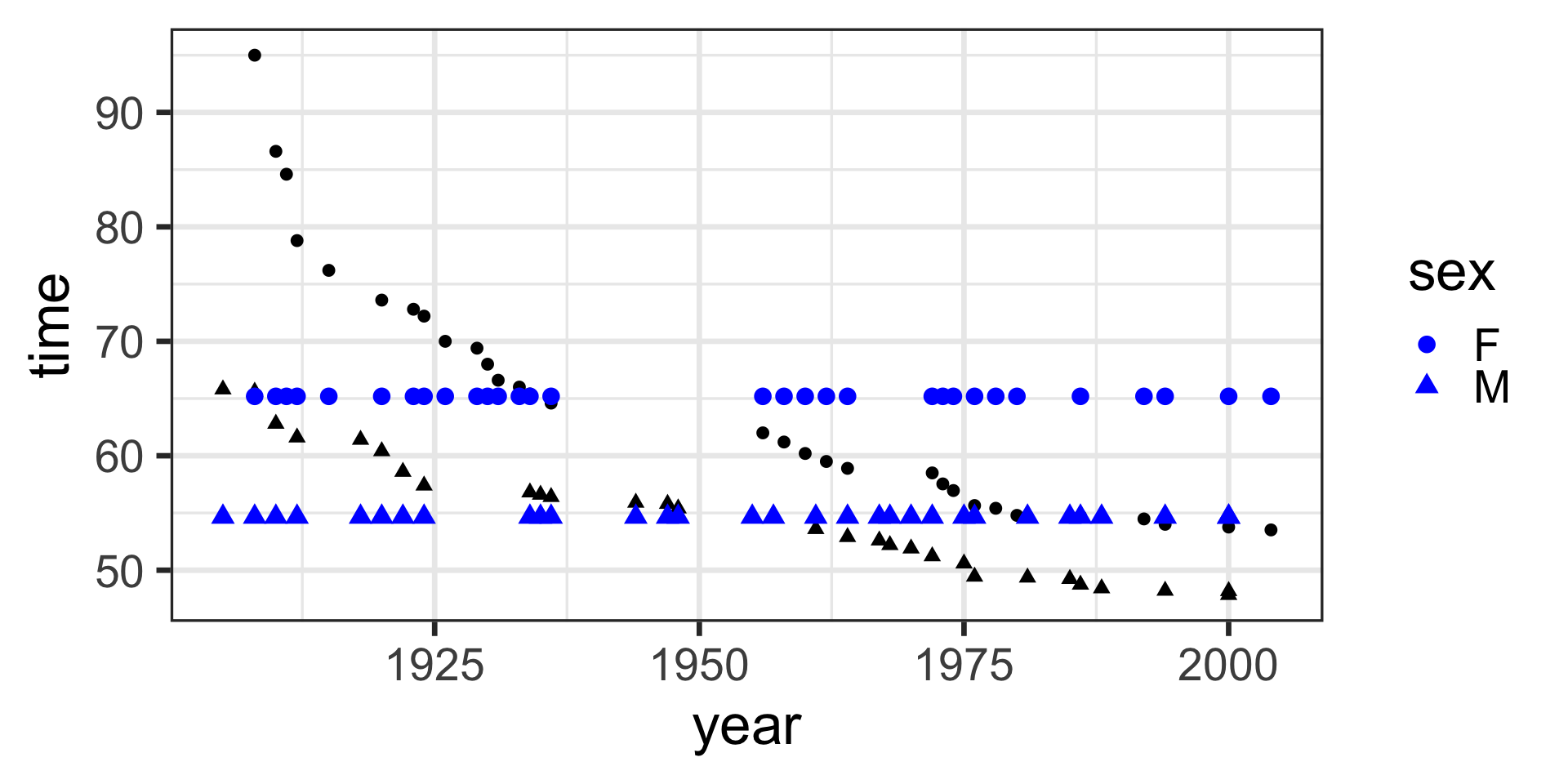
- in R:
y ~ 1 + year, in eq: \(y = w_1x_1 + w_2x_2 + w_3x_3\)
Data Science for Studying Language and the Mind
hereModel specificationSampling distribution and hypothesis testing with Correlation!
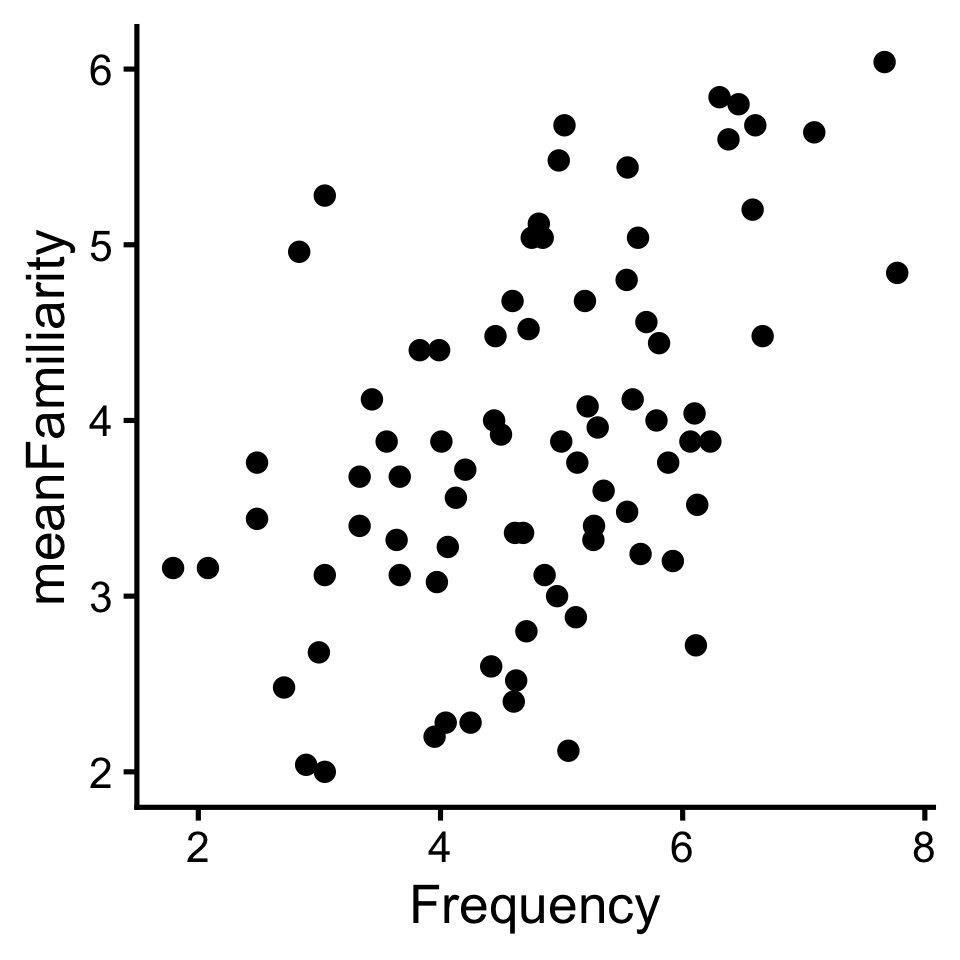
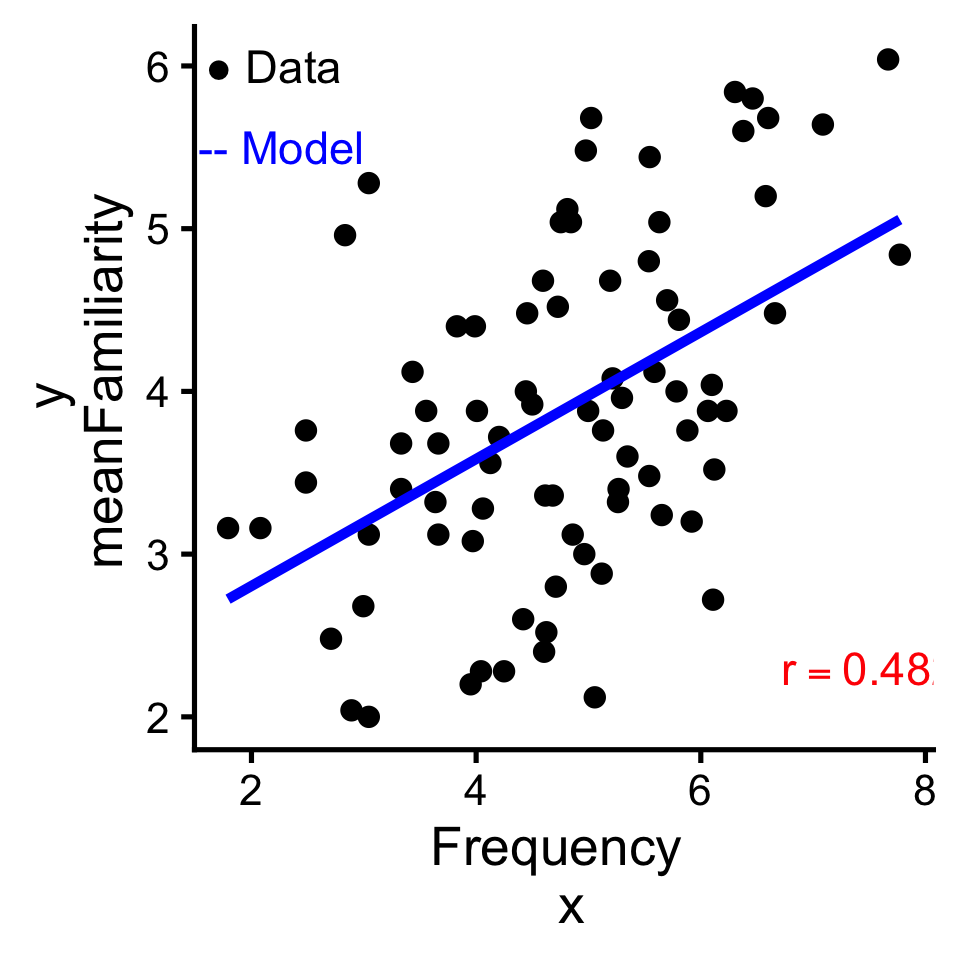
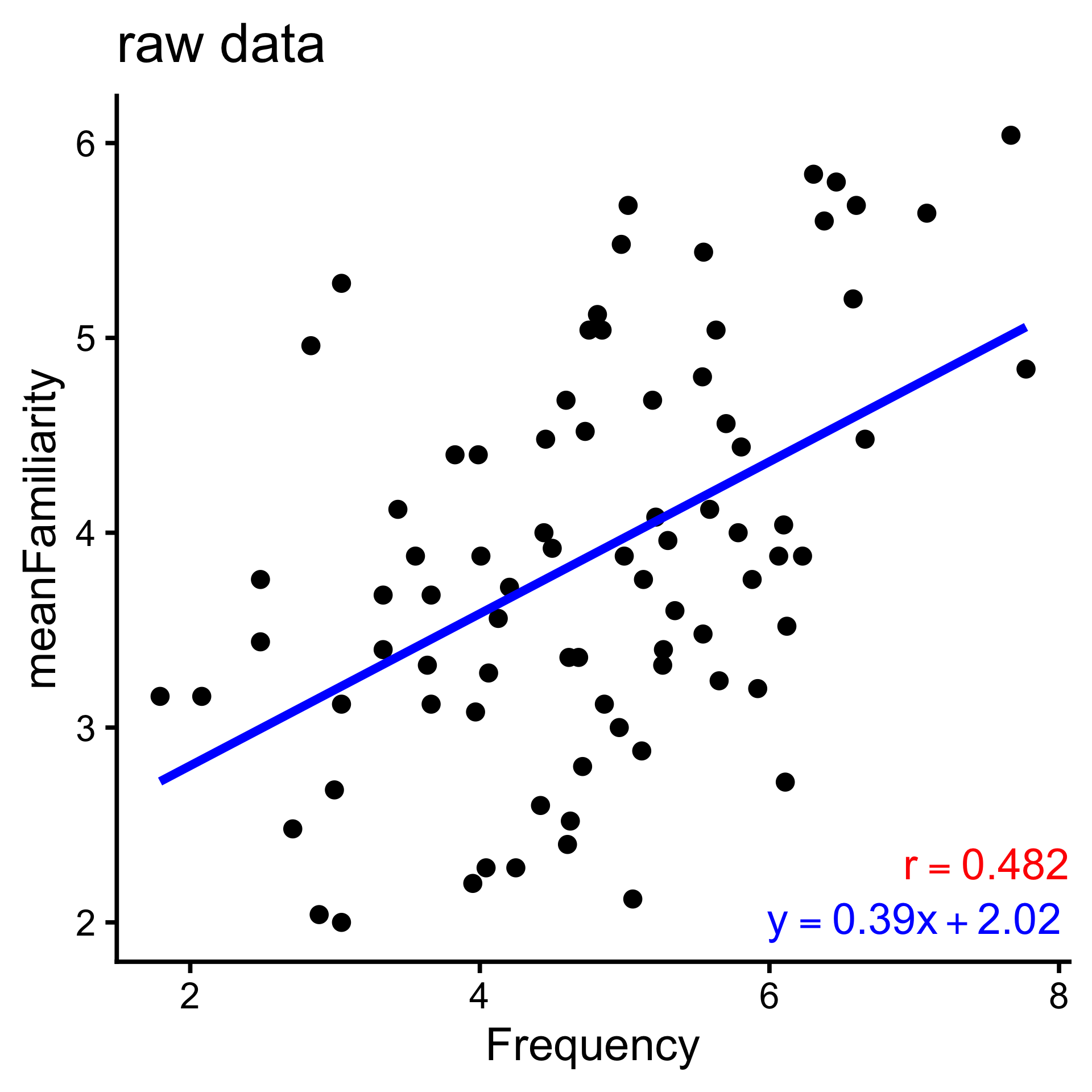
To review what we learned before break, let’s explore the relationship between Frequency and meanFamiliarity in the ratings dataset of the languageR package.

If there was no relationship, we’d say there are independent: knowing the value of one provides no information about about the other. But that’s not the case here.
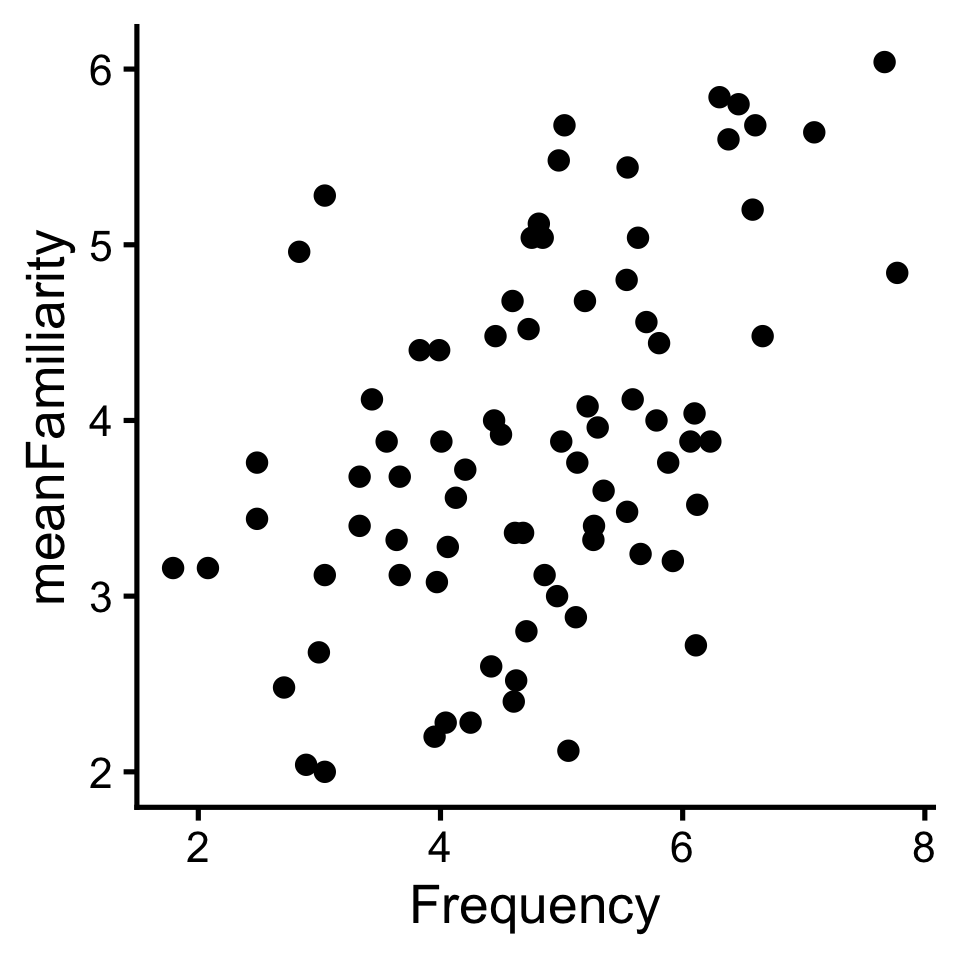
In a linear relationship, when one variable goes up the other goes up (positive); or when one goes up the other goes down (negative).
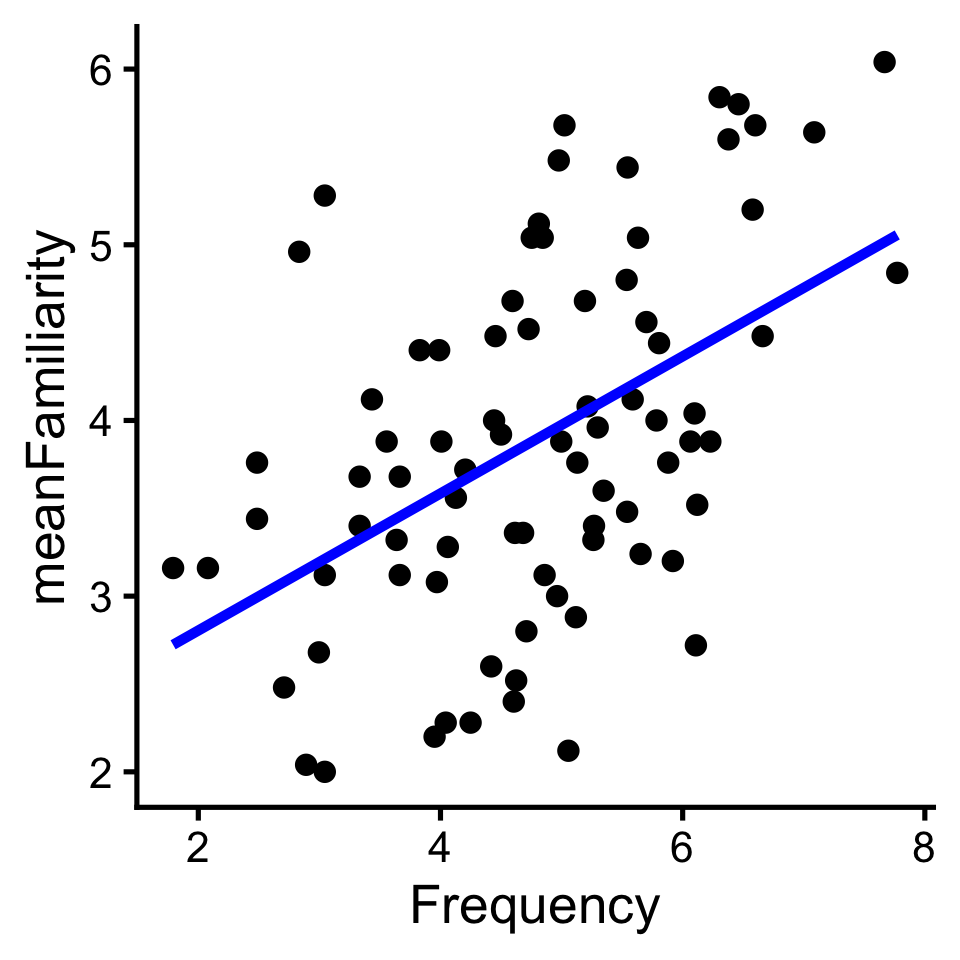
One way to quantify linear relationships is with correlation (\(r\)). Correlation expresses the linear relationship as a range from -1 (perfectly negative) to 1 (perfectly positive).
We can compute a correlation with R’s built in cor(x,y) function
Or via the infer pacakge.
Just like the mean — and all other test statistics! — \(r\) is subject to sampling variability. We can indicate our uncertainty around the correlation the same way we always have:
Construct the sampling distribution for the correlation:
Response: meanFamiliarity (numeric)
Explanatory: Frequency (numeric)
# A tibble: 6 × 2
replicate stat
<int> <dbl>
1 1 0.444
2 2 0.595
3 3 0.533
4 4 0.565
5 5 0.573
6 6 0.579Compute a confidence interval
Take a few minutes to try this yourself!
Use the infer way to visualize the sampling distribution and shade the confidence interval we just computed. Change the x-axis label to stat (correlation) as pictured below.
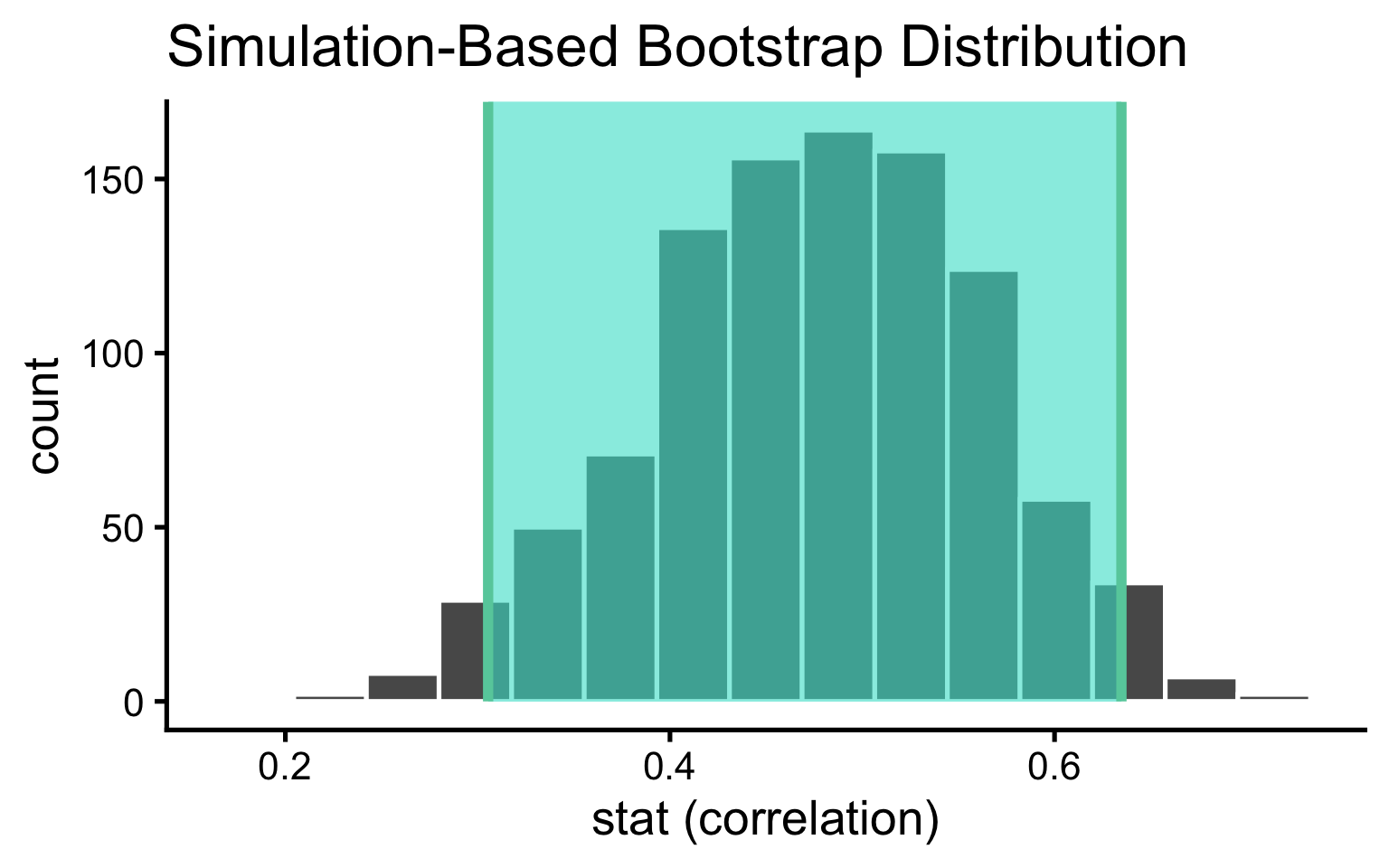
How do we test whether the correlation we observed is significantly different from zero? Hypothesis test!
Step 1: Construct the null distribution, the sampling distribution of the null hypothesis
Response: meanFamiliarity (numeric)
Explanatory: Frequency (numeric)
Null Hyp...
# A tibble: 6 × 2
replicate stat
<int> <dbl>
1 1 -0.189
2 2 0.0233
3 3 -0.0523
4 4 -0.0187
5 5 -0.0674
6 6 -0.0242Step 2: How likley is our observed value under the null? Get a p-value.
How do we test whether the correlation we observed is significantly different from zero? Hypothesis test!
Step 3: Decide whether to reject the null!
Interpret our p-value. Should we reject the null hypothesis?
Big picture overview of the model building process and the types of models we might encounter in our research.
Correlation is a simple case of model building, in which we use one value (\(x\)) to predict another (\(y\)).
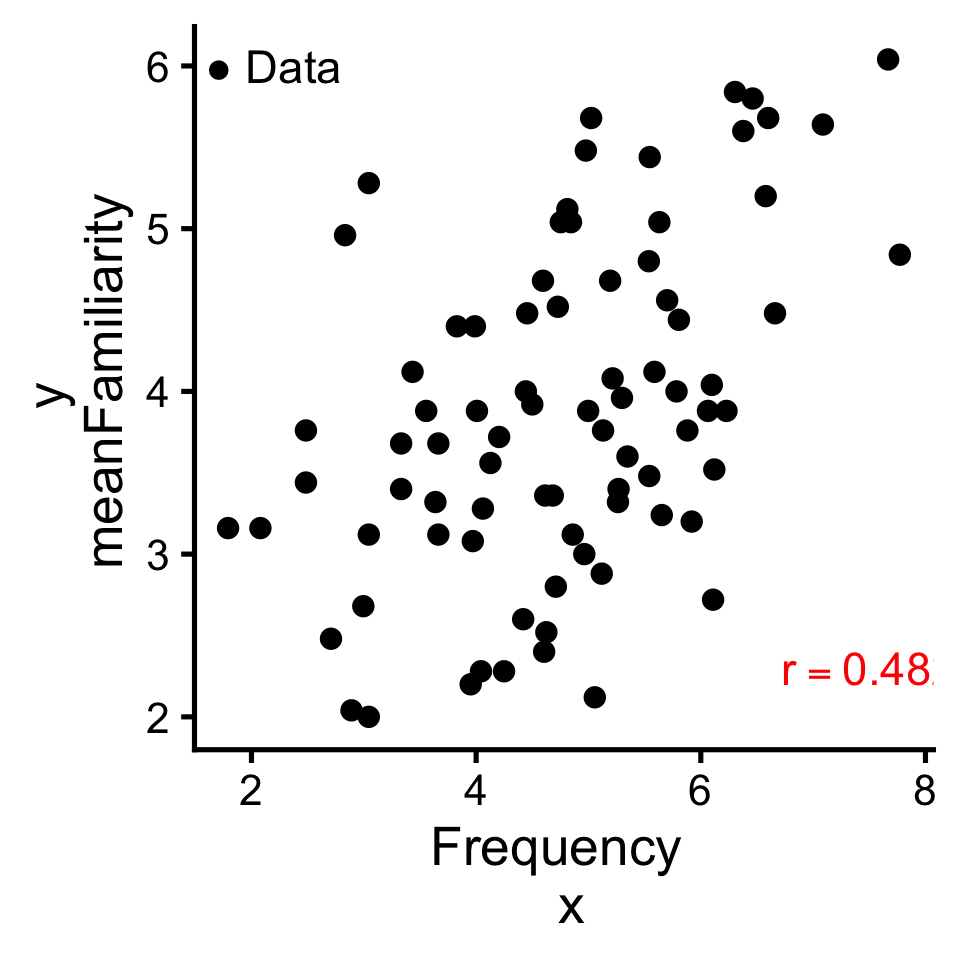
Even more specifically — formally, the model specification — we are fitting the linear model \(y = ax+b\), where \(a\) and \(b\) are free parameters.
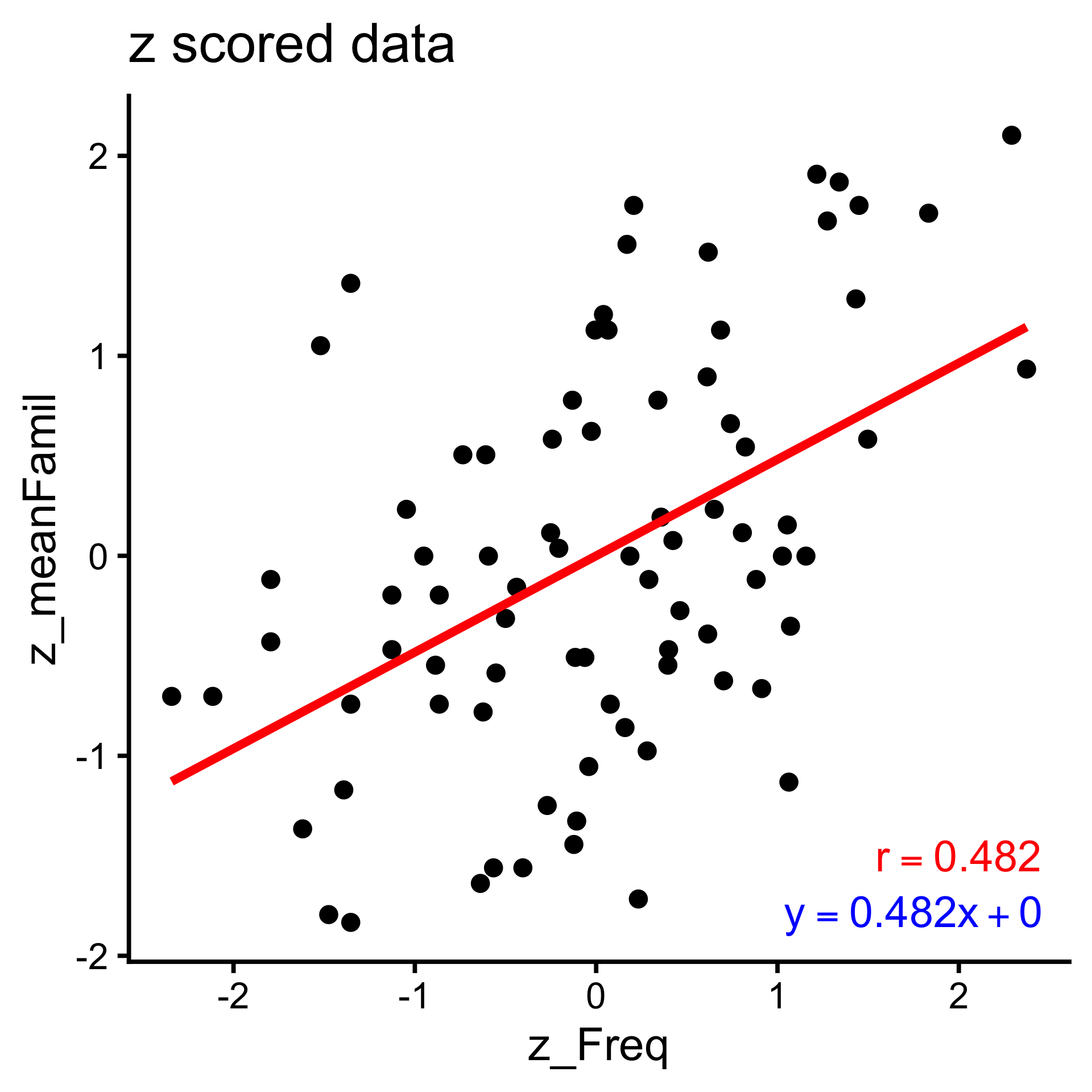
The link between correlation and linear models is understood when we normalize our variables with a z-score.
Frequency meanFamiliarity z_Freq z_meanFamil
1 4.204693 3.72 -0.4387602 -0.1573220
2 5.347108 3.60 0.4619516 -0.2742310
3 6.304449 5.84 1.2167459 1.9080703
4 3.828641 4.40 -0.7352500 0.5051623
5 3.663562 3.68 -0.8654029 -0.1962917
6 3.433987 4.12 -1.0464062 0.2323747Correlation is the slope of the line that best predicts \(y\) from \(x\) (after z-scoring)
Model specification (this week): specify the functional form of the model.Model fitting: you have the form, how do you estimate the free parameters?Model accuracy: you’ve estimated the parameters, how well does that model describe your data?Model reliability: when you estimate the parameters, you want to quantify your uncertainty on your estimatesTake a few minutes to try this yourself!
Ask ChatGPT what type of model it is made with?
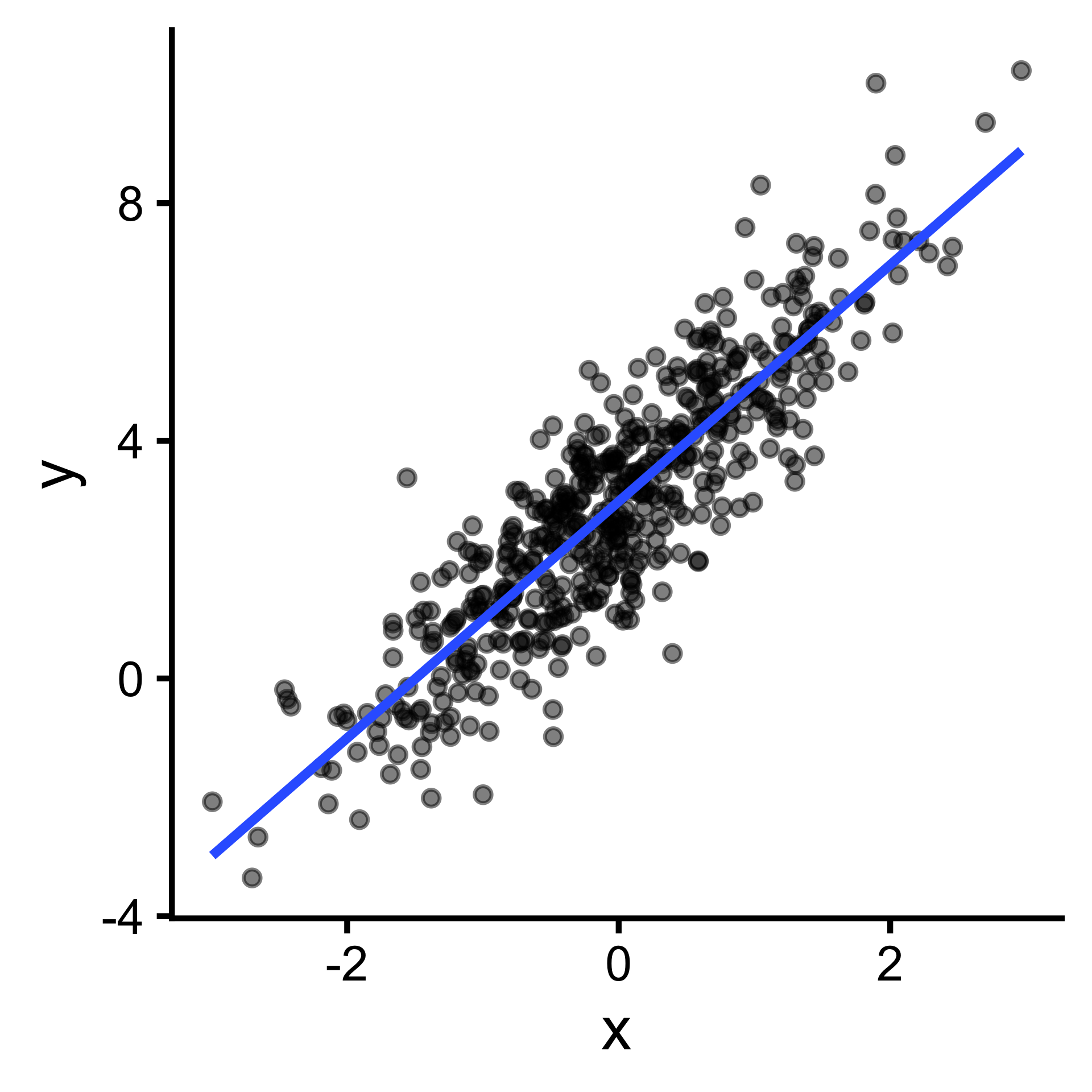
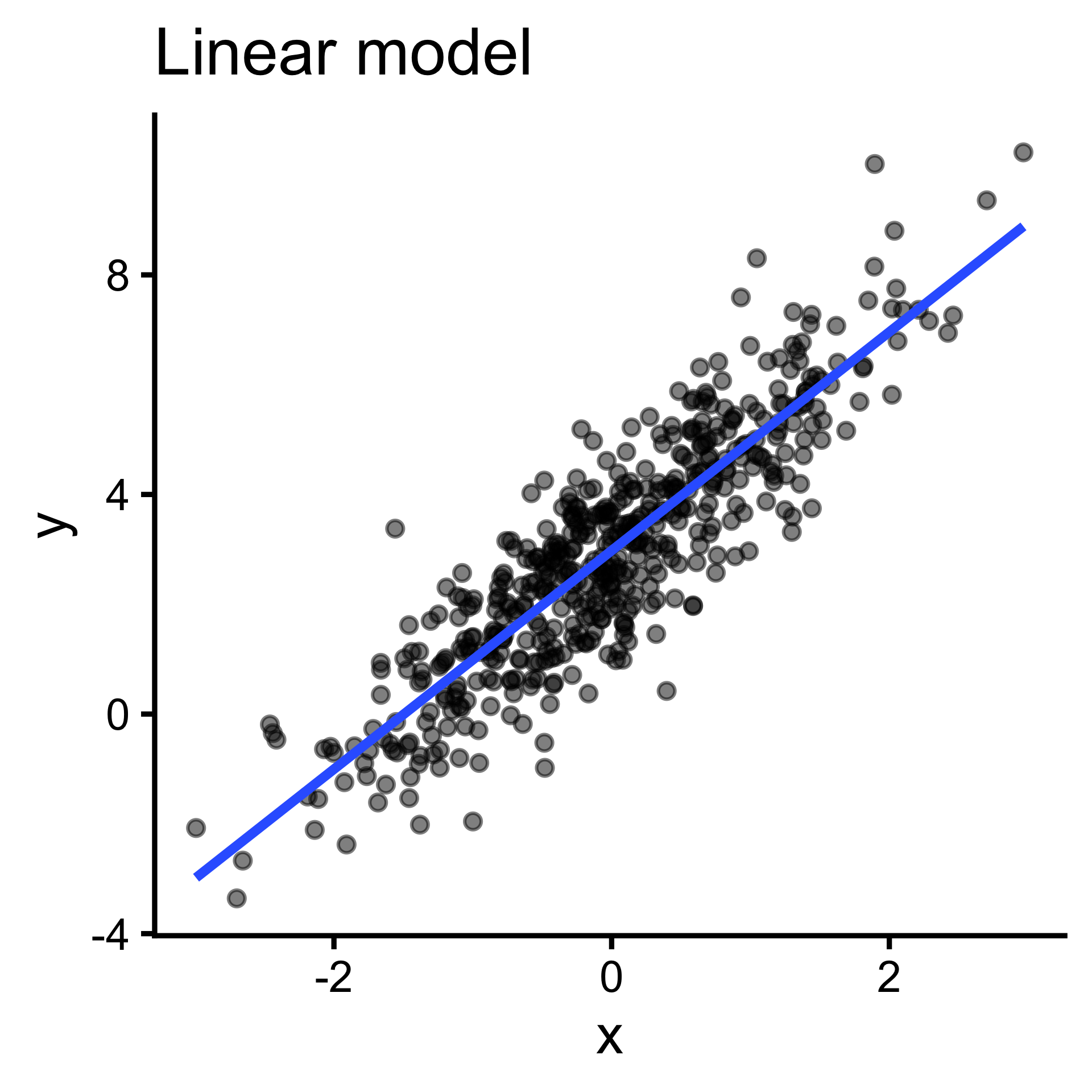
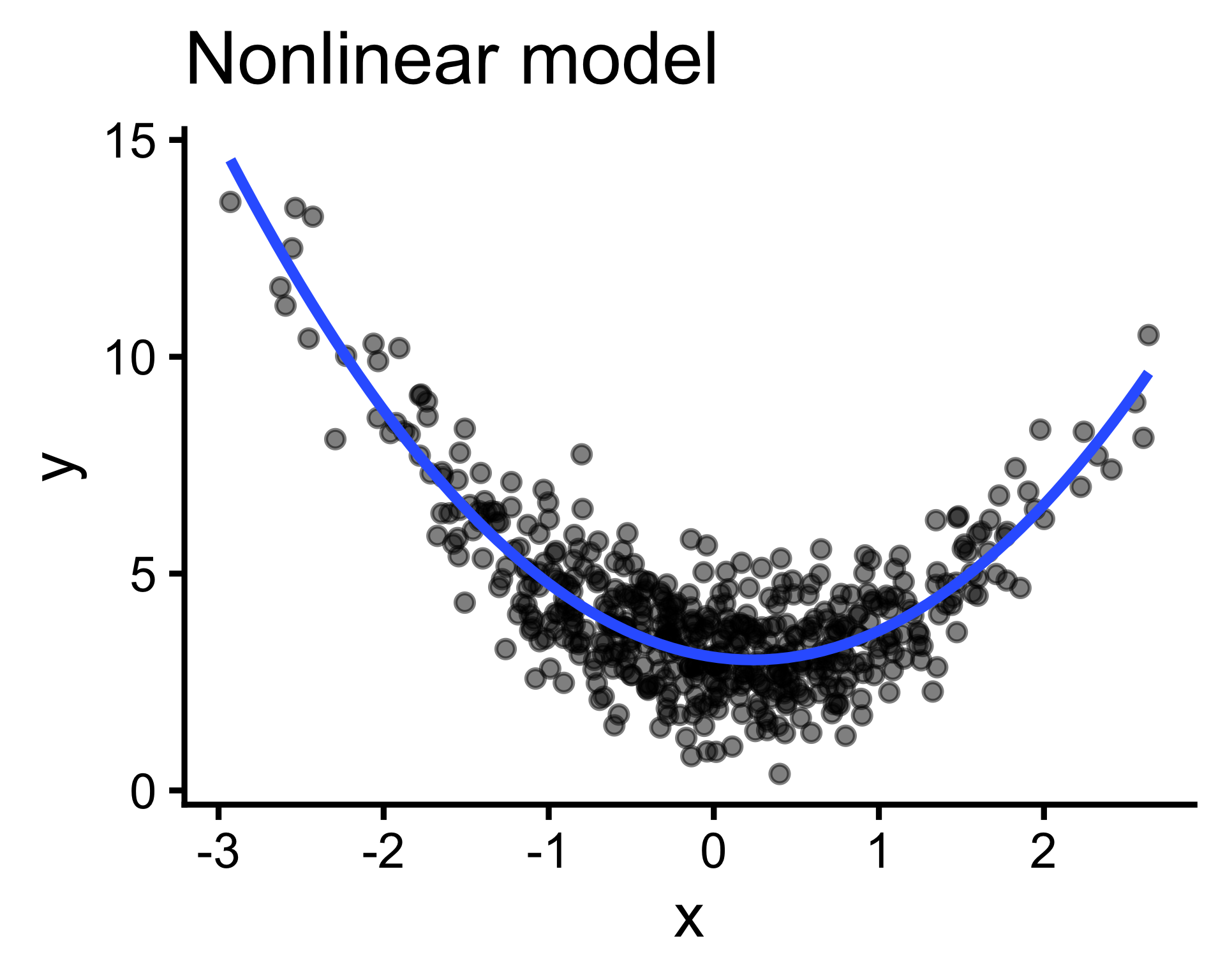
\(y = ax + b\) can be expressed \(y=\sum_{i=1}^{n}w_ix_i\)
Output (y) cannot be expressed as a weighted sum of inputs(\(y=\sum_{i=1}^{n}w_ix_i\) ); pattern is better captured by more complex functions. (But often we can linearize them!)
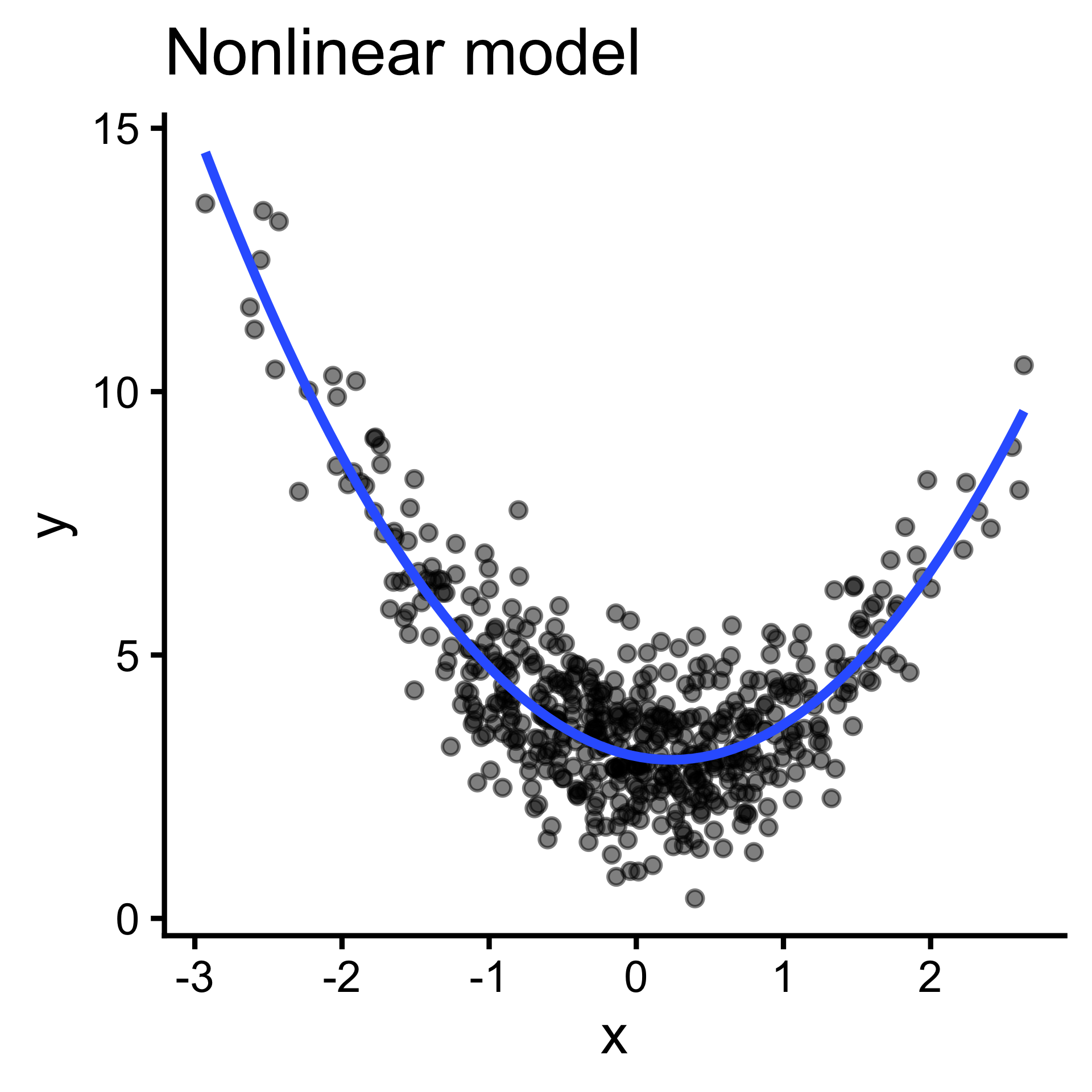
Take a few minutes to try this yourself!
Load the following data, which shows brain size and body weight for several different animals:
Explore the data to specify the type of model we should use to predict brain size by body weight.
Recall that model specification is one aspect of the model building process in which we select the form of the model (the type of model)
The following issues can also be considered part of the model specification process.
A well-specified model should be based on a clear understanding of the data, the underlying relationships, and the research question.
The linear model equation can be expressed in many ways, but they are all this same thing
To illustrate how this simple equation scales up to complex models, let’s start with a simple case (“toy”, “tractable”).
# A tibble: 2 × 2
x y
<dbl> <dbl>
1 1 3
2 2 5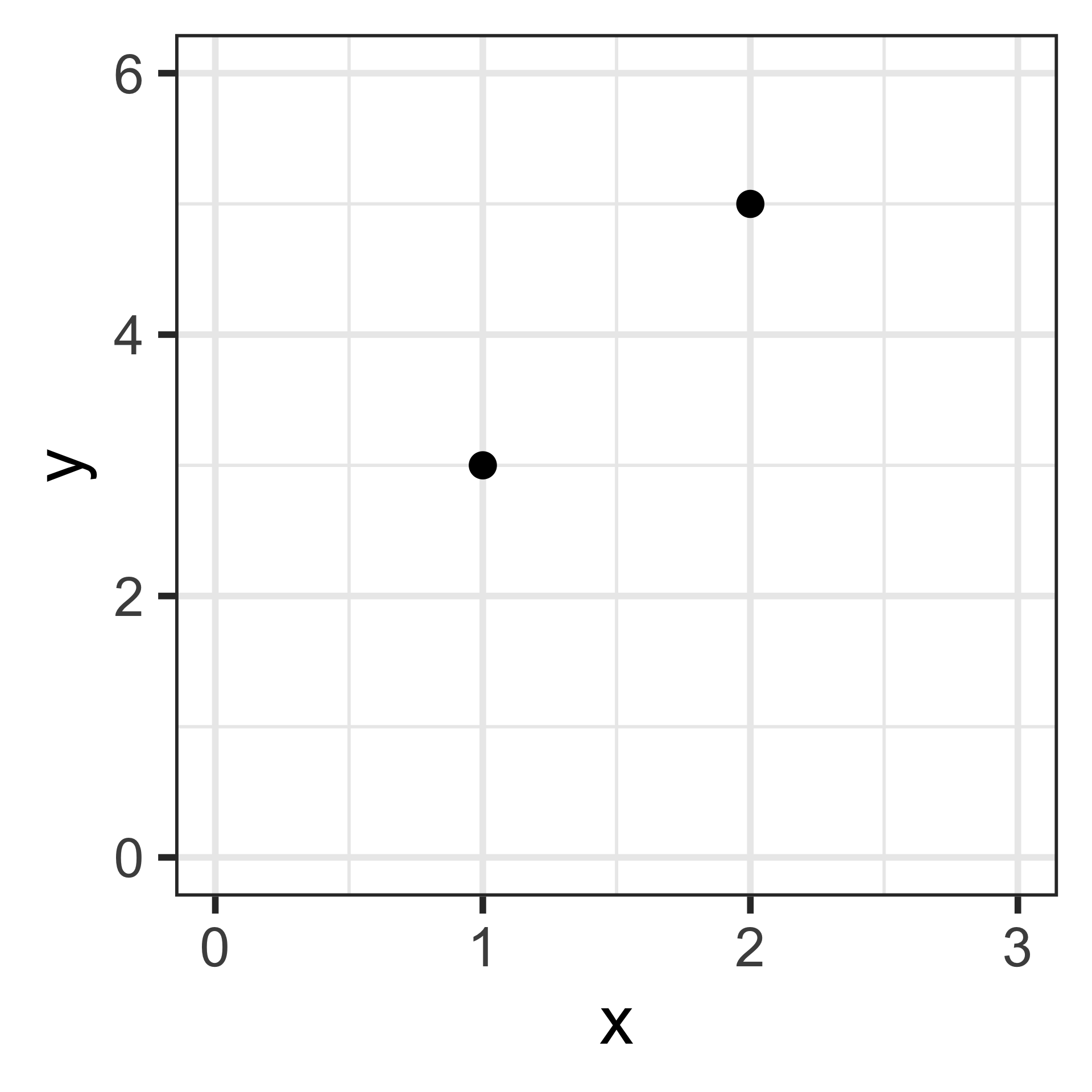
Specify our model!
Applied to a more complex problem
SwimRecordsHow have world swim records in the 100m changed over time?
Plot the swim records data, then use your model specification worksheet to specify the model.
What is the thing you are trying to understand?
What could explain the variation in your response variable?
Model terms describe how to include our explanatory variables in our model formula — there is more than one way!
y ~ 1, in eq: \(y=w_1x_1\)y ~ 1 + year, in eq: \(y = w_1x_1 + w_2x_2\)
y ~ 1 + sex, in eq: \(y = w_1x_1 + w_2x_2\)
y ~ 1 + year, in eq: \(y = w_1x_1 + w_2x_2 + w_3x_3\)
y ~ 1 + year + gender + year:gender
y ~ 1 + year * gendery ~ 1 + year * sex + I(year^2)Model specification (this week): specify the functional form of the model.Model fitting: you have the form, how do you estimate the free parameters?Model accuracy: you’ve estimated the parameters, how well does that model describe your data?Model reliability: when you estimate the parameters, you want to quantify your uncertainty on your estimates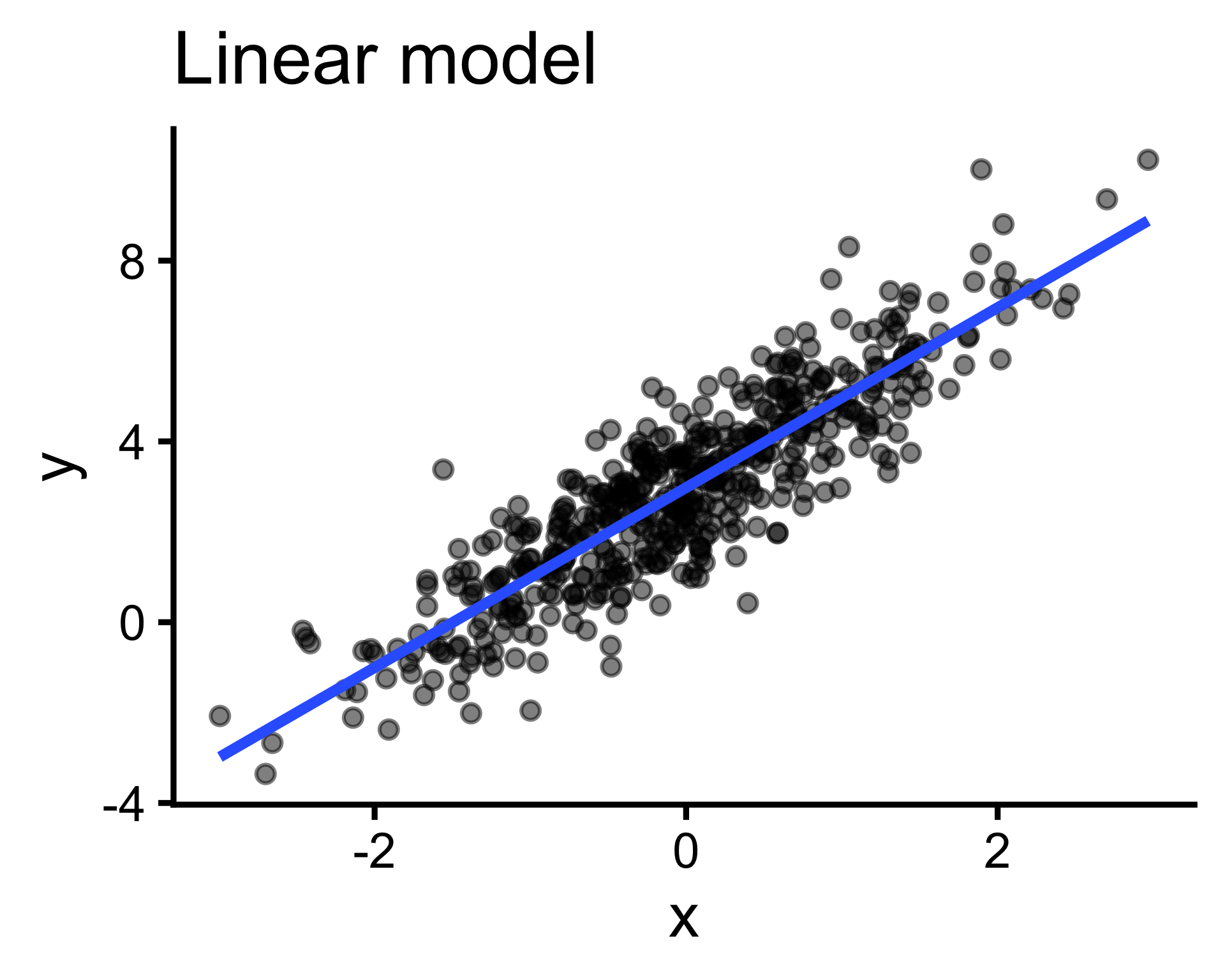
First aspect of the model building process in which we select the form of the model (the type of model)
Specify a model for the toy data. Then use lm() to fit the model.
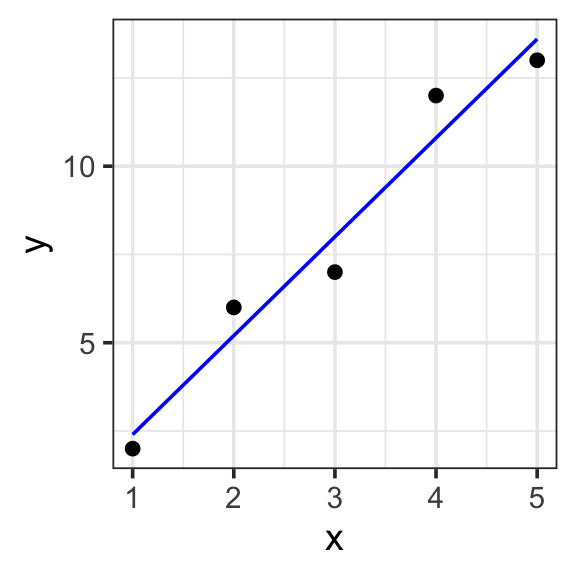
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{x}\)
Call:
lm(formula = y ~ 1 + x, data = toy_data)
Coefficients:
(Intercept) x
-0.4 2.8 Fitted model:
\(y = -0.4\cdot1 + 2.8\cdot x\)
| x | y | with_formula | with_predict |
|---|---|---|---|
| 1 | 2 | 2.4 | 2.4 |
| 2 | 6 | 5.2 | 5.2 |
| 3 | 7 | 8.0 | 8.0 |
| 4 | 12 | 10.8 | 10.8 |
| 5 | 13 | 13.6 | 13.6 |
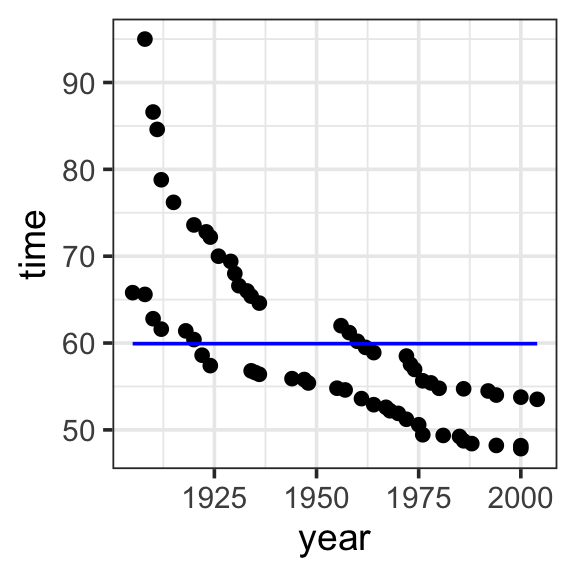
Model specification:
\(y = w_1\cdot\mathbf{1}\)
Call:
lm(formula = time ~ 1, data = SwimRecords)
Coefficients:
(Intercept)
59.92 Fitted model:
\(y = 59.92 \cdot 1\)
| year | time | sex | with_formula | with_predict |
|---|---|---|---|---|
| 1905 | 65.80 | M | 59.92 | 59.92419 |
| 1908 | 65.60 | M | 59.92 | 59.92419 |
| 1910 | 62.80 | M | 59.92 | 59.92419 |
| 1912 | 61.60 | M | 59.92 | 59.92419 |
| 1918 | 61.40 | M | 59.92 | 59.92419 |
| 1920 | 60.40 | M | 59.92 | 59.92419 |
| 1922 | 58.60 | M | 59.92 | 59.92419 |
| 1924 | 57.40 | M | 59.92 | 59.92419 |
| 1934 | 56.80 | M | 59.92 | 59.92419 |
| 1935 | 56.60 | M | 59.92 | 59.92419 |
| 1936 | 56.40 | M | 59.92 | 59.92419 |
| 1944 | 55.90 | M | 59.92 | 59.92419 |
| 1947 | 55.80 | M | 59.92 | 59.92419 |
| 1948 | 55.40 | M | 59.92 | 59.92419 |
| 1955 | 54.80 | M | 59.92 | 59.92419 |
| 1957 | 54.60 | M | 59.92 | 59.92419 |
| 1961 | 53.60 | M | 59.92 | 59.92419 |
| 1964 | 52.90 | M | 59.92 | 59.92419 |
| 1967 | 52.60 | M | 59.92 | 59.92419 |
| 1968 | 52.20 | M | 59.92 | 59.92419 |
| 1970 | 51.90 | M | 59.92 | 59.92419 |
| 1972 | 51.22 | M | 59.92 | 59.92419 |
| 1975 | 50.59 | M | 59.92 | 59.92419 |
| 1976 | 49.44 | M | 59.92 | 59.92419 |
| 1981 | 49.36 | M | 59.92 | 59.92419 |
| 1985 | 49.24 | M | 59.92 | 59.92419 |
| 1986 | 48.74 | M | 59.92 | 59.92419 |
| 1988 | 48.42 | M | 59.92 | 59.92419 |
| 1994 | 48.21 | M | 59.92 | 59.92419 |
| 2000 | 48.18 | M | 59.92 | 59.92419 |
| 2000 | 47.84 | M | 59.92 | 59.92419 |
| 1908 | 95.00 | F | 59.92 | 59.92419 |
| 1910 | 86.60 | F | 59.92 | 59.92419 |
| 1911 | 84.60 | F | 59.92 | 59.92419 |
| 1912 | 78.80 | F | 59.92 | 59.92419 |
| 1915 | 76.20 | F | 59.92 | 59.92419 |
| 1920 | 73.60 | F | 59.92 | 59.92419 |
| 1923 | 72.80 | F | 59.92 | 59.92419 |
| 1924 | 72.20 | F | 59.92 | 59.92419 |
| 1926 | 70.00 | F | 59.92 | 59.92419 |
| 1929 | 69.40 | F | 59.92 | 59.92419 |
| 1930 | 68.00 | F | 59.92 | 59.92419 |
| 1931 | 66.60 | F | 59.92 | 59.92419 |
| 1933 | 66.00 | F | 59.92 | 59.92419 |
| 1934 | 65.40 | F | 59.92 | 59.92419 |
| 1936 | 64.60 | F | 59.92 | 59.92419 |
| 1956 | 62.00 | F | 59.92 | 59.92419 |
| 1958 | 61.20 | F | 59.92 | 59.92419 |
| 1960 | 60.20 | F | 59.92 | 59.92419 |
| 1962 | 59.50 | F | 59.92 | 59.92419 |
| 1964 | 58.90 | F | 59.92 | 59.92419 |
| 1972 | 58.50 | F | 59.92 | 59.92419 |
| 1973 | 57.54 | F | 59.92 | 59.92419 |
| 1974 | 56.96 | F | 59.92 | 59.92419 |
| 1976 | 55.65 | F | 59.92 | 59.92419 |
| 1978 | 55.41 | F | 59.92 | 59.92419 |
| 1980 | 54.79 | F | 59.92 | 59.92419 |
| 1986 | 54.73 | F | 59.92 | 59.92419 |
| 1992 | 54.48 | F | 59.92 | 59.92419 |
| 1994 | 54.01 | F | 59.92 | 59.92419 |
| 2000 | 53.77 | F | 59.92 | 59.92419 |
| 2004 | 53.52 | F | 59.92 | 59.92419 |
model <- lm(time ~ 1, data = SwimRecords)
SwimRecords_predict <- SwimRecords %>%
mutate(with_formula = 59.92*1) %>%
mutate(with_predict= predict(model, SwimRecords))
SwimRecords_predict %>%
ggplot(aes(x = year, y = time)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) Specify a model for the SwimRecords data that includes the intercept and the year. Use lm() to fit the model. Then use predict() to get the models prediction.
If you have time, plot the data and model predictions with ggplot().
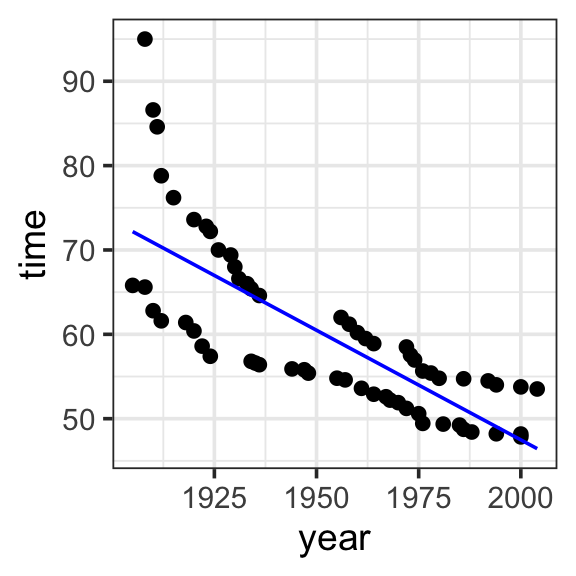
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{year}\)
Call:
lm(formula = time ~ 1 + year, data = SwimRecords)
Coefficients:
(Intercept) year
567.2420 -0.2599 Fitted model:
\(y = 567.2420 \cdot \mathbf{1} + -0.2599 \cdot \mathbf{year}\)
| year | time | sex | with_formula | with_predict |
|---|---|---|---|---|
| 1905 | 65.80 | M | 72.1325 | 72.17614 |
| 1908 | 65.60 | M | 71.3528 | 71.39651 |
| 1910 | 62.80 | M | 70.8330 | 70.87676 |
| 1912 | 61.60 | M | 70.3132 | 70.35700 |
| 1918 | 61.40 | M | 68.7538 | 68.79774 |
| 1920 | 60.40 | M | 68.2340 | 68.27798 |
| 1922 | 58.60 | M | 67.7142 | 67.75823 |
| 1924 | 57.40 | M | 67.1944 | 67.23848 |
| 1934 | 56.80 | M | 64.5954 | 64.63971 |
| 1935 | 56.60 | M | 64.3355 | 64.37983 |
| 1936 | 56.40 | M | 64.0756 | 64.11995 |
| 1944 | 55.90 | M | 61.9964 | 62.04093 |
| 1947 | 55.80 | M | 61.2167 | 61.26130 |
| 1948 | 55.40 | M | 60.9568 | 61.00143 |
| 1955 | 54.80 | M | 59.1375 | 59.18229 |
| 1957 | 54.60 | M | 58.6177 | 58.66253 |
| 1961 | 53.60 | M | 57.5781 | 57.62302 |
| 1964 | 52.90 | M | 56.7984 | 56.84339 |
| 1967 | 52.60 | M | 56.0187 | 56.06376 |
| 1968 | 52.20 | M | 55.7588 | 55.80388 |
| 1970 | 51.90 | M | 55.2390 | 55.28413 |
| 1972 | 51.22 | M | 54.7192 | 54.76438 |
| 1975 | 50.59 | M | 53.9395 | 53.98474 |
| 1976 | 49.44 | M | 53.6796 | 53.72487 |
| 1981 | 49.36 | M | 52.3801 | 52.42548 |
| 1985 | 49.24 | M | 51.3405 | 51.38597 |
| 1986 | 48.74 | M | 51.0806 | 51.12610 |
| 1988 | 48.42 | M | 50.5608 | 50.60634 |
| 1994 | 48.21 | M | 49.0014 | 49.04708 |
| 2000 | 48.18 | M | 47.4420 | 47.48782 |
| 2000 | 47.84 | M | 47.4420 | 47.48782 |
| 1908 | 95.00 | F | 71.3528 | 71.39651 |
| 1910 | 86.60 | F | 70.8330 | 70.87676 |
| 1911 | 84.60 | F | 70.5731 | 70.61688 |
| 1912 | 78.80 | F | 70.3132 | 70.35700 |
| 1915 | 76.20 | F | 69.5335 | 69.57737 |
| 1920 | 73.60 | F | 68.2340 | 68.27798 |
| 1923 | 72.80 | F | 67.4543 | 67.49835 |
| 1924 | 72.20 | F | 67.1944 | 67.23848 |
| 1926 | 70.00 | F | 66.6746 | 66.71872 |
| 1929 | 69.40 | F | 65.8949 | 65.93909 |
| 1930 | 68.00 | F | 65.6350 | 65.67921 |
| 1931 | 66.60 | F | 65.3751 | 65.41934 |
| 1933 | 66.00 | F | 64.8553 | 64.89958 |
| 1934 | 65.40 | F | 64.5954 | 64.63971 |
| 1936 | 64.60 | F | 64.0756 | 64.11995 |
| 1956 | 62.00 | F | 58.8776 | 58.92241 |
| 1958 | 61.20 | F | 58.3578 | 58.40266 |
| 1960 | 60.20 | F | 57.8380 | 57.88290 |
| 1962 | 59.50 | F | 57.3182 | 57.36315 |
| 1964 | 58.90 | F | 56.7984 | 56.84339 |
| 1972 | 58.50 | F | 54.7192 | 54.76438 |
| 1973 | 57.54 | F | 54.4593 | 54.50450 |
| 1974 | 56.96 | F | 54.1994 | 54.24462 |
| 1976 | 55.65 | F | 53.6796 | 53.72487 |
| 1978 | 55.41 | F | 53.1598 | 53.20511 |
| 1980 | 54.79 | F | 52.6400 | 52.68536 |
| 1986 | 54.73 | F | 51.0806 | 51.12610 |
| 1992 | 54.48 | F | 49.5212 | 49.56683 |
| 1994 | 54.01 | F | 49.0014 | 49.04708 |
| 2000 | 53.77 | F | 47.4420 | 47.48782 |
| 2004 | 53.52 | F | 46.4024 | 46.44831 |
model <- lm(time ~ 1 + year, data = SwimRecords)
SwimRecords_predict <- SwimRecords %>%
mutate(with_formula = 567.2420*1 + -0.2599*year) %>%
mutate(with_predict= predict(model, SwimRecords))
SwimRecords_predict %>%
ggplot(aes(x = year, y = time)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) 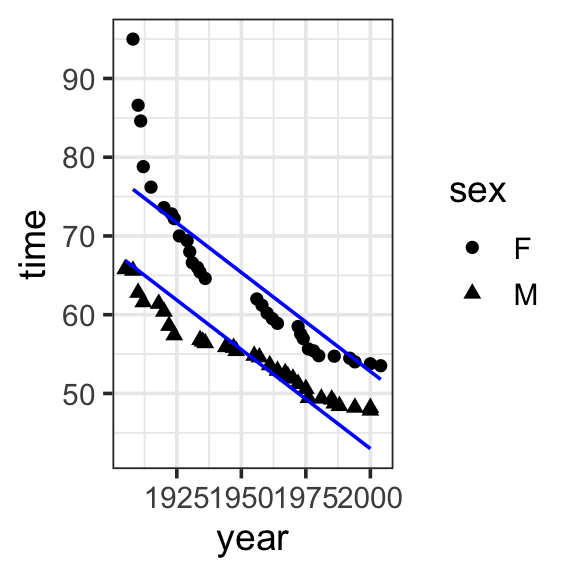
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{year} + w_3\cdot\mathbf{sex}\)
Call:
lm(formula = time ~ 1 + year + sex, data = SwimRecords)
Coefficients:
(Intercept) year sexM
555.7168 -0.2515 -9.7980 Fitted model:
\(y = 555.7168 \cdot \mathbf{1} + -0.2515 \cdot \mathbf{year} + -9.7980 \cdot \mathbf{sex}\)
| year | time | sex | sex_numeric | with_formula | with_predict |
|---|---|---|---|---|---|
| 1905 | 65.80 | M | 1 | 66.8113 | 66.88051 |
| 1908 | 65.60 | M | 1 | 66.0568 | 66.12612 |
| 1910 | 62.80 | M | 1 | 65.5538 | 65.62319 |
| 1912 | 61.60 | M | 1 | 65.0508 | 65.12026 |
| 1918 | 61.40 | M | 1 | 63.5418 | 63.61148 |
| 1920 | 60.40 | M | 1 | 63.0388 | 63.10855 |
| 1922 | 58.60 | M | 1 | 62.5358 | 62.60563 |
| 1924 | 57.40 | M | 1 | 62.0328 | 62.10270 |
| 1934 | 56.80 | M | 1 | 59.5178 | 59.58806 |
| 1935 | 56.60 | M | 1 | 59.2663 | 59.33660 |
| 1936 | 56.40 | M | 1 | 59.0148 | 59.08513 |
| 1944 | 55.90 | M | 1 | 57.0028 | 57.07343 |
| 1947 | 55.80 | M | 1 | 56.2483 | 56.31903 |
| 1948 | 55.40 | M | 1 | 55.9968 | 56.06757 |
| 1955 | 54.80 | M | 1 | 54.2363 | 54.30732 |
| 1957 | 54.60 | M | 1 | 53.7333 | 53.80440 |
| 1961 | 53.60 | M | 1 | 52.7273 | 52.79854 |
| 1964 | 52.90 | M | 1 | 51.9728 | 52.04415 |
| 1967 | 52.60 | M | 1 | 51.2183 | 51.28976 |
| 1968 | 52.20 | M | 1 | 50.9668 | 51.03830 |
| 1970 | 51.90 | M | 1 | 50.4638 | 50.53537 |
| 1972 | 51.22 | M | 1 | 49.9608 | 50.03244 |
| 1975 | 50.59 | M | 1 | 49.2063 | 49.27805 |
| 1976 | 49.44 | M | 1 | 48.9548 | 49.02659 |
| 1981 | 49.36 | M | 1 | 47.6973 | 47.76927 |
| 1985 | 49.24 | M | 1 | 46.6913 | 46.76341 |
| 1986 | 48.74 | M | 1 | 46.4398 | 46.51195 |
| 1988 | 48.42 | M | 1 | 45.9368 | 46.00902 |
| 1994 | 48.21 | M | 1 | 44.4278 | 44.50024 |
| 2000 | 48.18 | M | 1 | 42.9188 | 42.99146 |
| 2000 | 47.84 | M | 1 | 42.9188 | 42.99146 |
| 1908 | 95.00 | F | 0 | 75.8548 | 75.92408 |
| 1910 | 86.60 | F | 0 | 75.3518 | 75.42115 |
| 1911 | 84.60 | F | 0 | 75.1003 | 75.16969 |
| 1912 | 78.80 | F | 0 | 74.8488 | 74.91822 |
| 1915 | 76.20 | F | 0 | 74.0943 | 74.16383 |
| 1920 | 73.60 | F | 0 | 72.8368 | 72.90651 |
| 1923 | 72.80 | F | 0 | 72.0823 | 72.15212 |
| 1924 | 72.20 | F | 0 | 71.8308 | 71.90066 |
| 1926 | 70.00 | F | 0 | 71.3278 | 71.39773 |
| 1929 | 69.40 | F | 0 | 70.5733 | 70.64334 |
| 1930 | 68.00 | F | 0 | 70.3218 | 70.39188 |
| 1931 | 66.60 | F | 0 | 70.0703 | 70.14041 |
| 1933 | 66.00 | F | 0 | 69.5673 | 69.63749 |
| 1934 | 65.40 | F | 0 | 69.3158 | 69.38602 |
| 1936 | 64.60 | F | 0 | 68.8128 | 68.88310 |
| 1956 | 62.00 | F | 0 | 63.7828 | 63.85382 |
| 1958 | 61.20 | F | 0 | 63.2798 | 63.35090 |
| 1960 | 60.20 | F | 0 | 62.7768 | 62.84797 |
| 1962 | 59.50 | F | 0 | 62.2738 | 62.34504 |
| 1964 | 58.90 | F | 0 | 61.7708 | 61.84211 |
| 1972 | 58.50 | F | 0 | 59.7588 | 59.83040 |
| 1973 | 57.54 | F | 0 | 59.5073 | 59.57894 |
| 1974 | 56.96 | F | 0 | 59.2558 | 59.32748 |
| 1976 | 55.65 | F | 0 | 58.7528 | 58.82455 |
| 1978 | 55.41 | F | 0 | 58.2498 | 58.32162 |
| 1980 | 54.79 | F | 0 | 57.7468 | 57.81869 |
| 1986 | 54.73 | F | 0 | 56.2378 | 56.30991 |
| 1992 | 54.48 | F | 0 | 54.7288 | 54.80113 |
| 1994 | 54.01 | F | 0 | 54.2258 | 54.29820 |
| 2000 | 53.77 | F | 0 | 52.7168 | 52.78942 |
| 2004 | 53.52 | F | 0 | 51.7108 | 51.78357 |
model <- lm(time ~ 1 + year + sex, data = SwimRecords)
SwimRecords_predict <- SwimRecords %>%
mutate(sex_numeric = case_when(
sex == 'M' ~ 1,
sex == 'F' ~ 0
)) %>%
mutate(with_formula = 555.7168*1 + -0.2515*year + -9.7980 *sex_numeric) %>%
mutate(with_predict= predict(model, SwimRecords))
SwimRecords_predict %>%
ggplot(aes(x = year, y = time, shape = sex)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) We specified the model including intercept, year, and sex as follows:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{year} + w_3\cdot\mathbf{sex}\)
Fit the model with infer this time. What are the following weights:
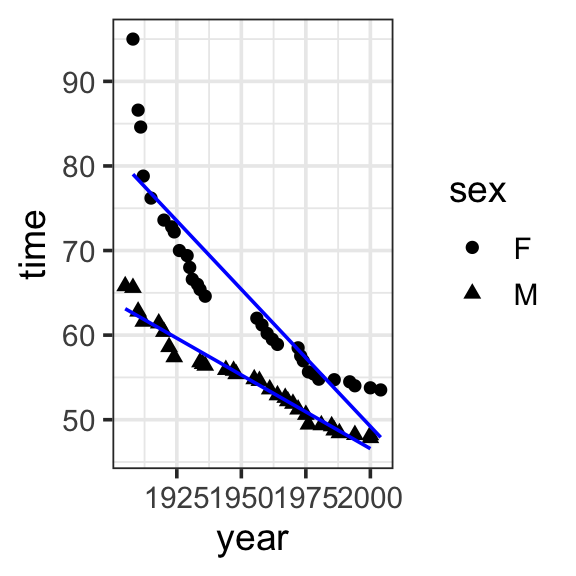
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{year} + w_3\cdot\mathbf{sex} + w_4\cdot\mathbf{year\times{sex}}\)
Call:
lm(formula = time ~ 1 + year * sex, data = SwimRecords)
Coefficients:
(Intercept) year sexM year:sexM
697.3012 -0.3240 -302.4638 0.1499 Fitted model:
\[\begin{align}
y = &697.3012 \cdot \mathbf{1} + -0.3240 \cdot \mathbf{year} + -302.4638 \cdot \mathbf{sex}\\
&+ 0.1499 \cdot \mathbf{year\times{sex}}
\end{align}\]
| year | time | sex | with_predict |
|---|---|---|---|
| 1905 | 65.80 | M | 63.12106 |
| 1908 | 65.60 | M | 62.59867 |
| 1910 | 62.80 | M | 62.25041 |
| 1912 | 61.60 | M | 61.90215 |
| 1918 | 61.40 | M | 60.85738 |
| 1920 | 60.40 | M | 60.50912 |
| 1922 | 58.60 | M | 60.16086 |
| 1924 | 57.40 | M | 59.81260 |
| 1934 | 56.80 | M | 58.07131 |
| 1935 | 56.60 | M | 57.89718 |
| 1936 | 56.40 | M | 57.72305 |
| 1944 | 55.90 | M | 56.33002 |
| 1947 | 55.80 | M | 55.80763 |
| 1948 | 55.40 | M | 55.63350 |
| 1955 | 54.80 | M | 54.41459 |
| 1957 | 54.60 | M | 54.06634 |
| 1961 | 53.60 | M | 53.36982 |
| 1964 | 52.90 | M | 52.84743 |
| 1967 | 52.60 | M | 52.32504 |
| 1968 | 52.20 | M | 52.15091 |
| 1970 | 51.90 | M | 51.80266 |
| 1972 | 51.22 | M | 51.45440 |
| 1975 | 50.59 | M | 50.93201 |
| 1976 | 49.44 | M | 50.75788 |
| 1981 | 49.36 | M | 49.88723 |
| 1985 | 49.24 | M | 49.19072 |
| 1986 | 48.74 | M | 49.01659 |
| 1988 | 48.42 | M | 48.66833 |
| 1994 | 48.21 | M | 47.62355 |
| 2000 | 48.18 | M | 46.57878 |
| 2000 | 47.84 | M | 46.57878 |
| 1908 | 95.00 | F | 79.02170 |
| 1910 | 86.60 | F | 78.37361 |
| 1911 | 84.60 | F | 78.04956 |
| 1912 | 78.80 | F | 77.72552 |
| 1915 | 76.20 | F | 76.75338 |
| 1920 | 73.60 | F | 75.13315 |
| 1923 | 72.80 | F | 74.16101 |
| 1924 | 72.20 | F | 73.83697 |
| 1926 | 70.00 | F | 73.18887 |
| 1929 | 69.40 | F | 72.21674 |
| 1930 | 68.00 | F | 71.89269 |
| 1931 | 66.60 | F | 71.56864 |
| 1933 | 66.00 | F | 70.92055 |
| 1934 | 65.40 | F | 70.59651 |
| 1936 | 64.60 | F | 69.94842 |
| 1956 | 62.00 | F | 63.46750 |
| 1958 | 61.20 | F | 62.81941 |
| 1960 | 60.20 | F | 62.17131 |
| 1962 | 59.50 | F | 61.52322 |
| 1964 | 58.90 | F | 60.87513 |
| 1972 | 58.50 | F | 58.28276 |
| 1973 | 57.54 | F | 57.95872 |
| 1974 | 56.96 | F | 57.63467 |
| 1976 | 55.65 | F | 56.98658 |
| 1978 | 55.41 | F | 56.33849 |
| 1980 | 54.79 | F | 55.69040 |
| 1986 | 54.73 | F | 53.74612 |
| 1992 | 54.48 | F | 51.80185 |
| 1994 | 54.01 | F | 51.15375 |
| 2000 | 53.77 | F | 49.20948 |
| 2004 | 53.52 | F | 47.91330 |
model <- lm(time ~ 1 + year * sex, data = SwimRecords)
SwimRecords_predict <- SwimRecords %>%
mutate(with_predict= predict(model, SwimRecords))
SwimRecords_predict %>%
ggplot(aes(x = year, y = time, shape = sex)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) 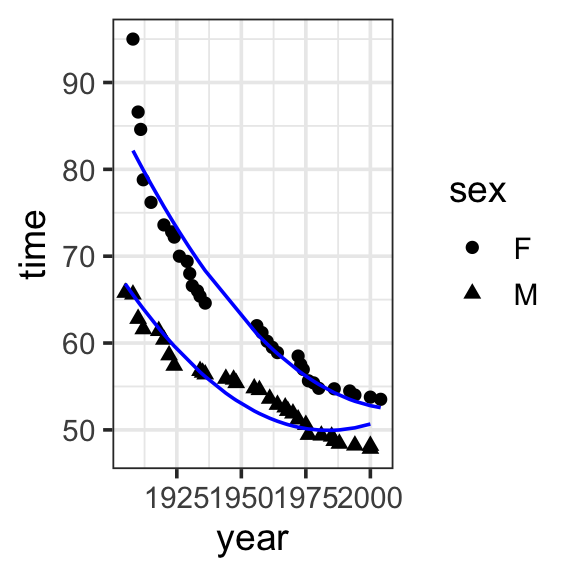
Model specification:
\[\begin{align}
y = &w_1\cdot\mathbf{1} + w_2\cdot\mathbf{year} + w_3\cdot\mathbf{sex} \\
&+ w_4\cdot\mathbf{year\times{sex}} +w_5\cdot\mathbf{year}^2
\end{align}\]
Call:
lm(formula = time ~ 1 + year * sex + I(year^2), data = SwimRecords)
Coefficients:
(Intercept) year sexM I(year^2) year:sexM
1.110e+04 -1.098e+01 -3.171e+02 2.729e-03 1.575e-01 Fitted model:
\[\begin{align}
y = &11100 \cdot \mathbf{1} + -10.98 \cdot \mathbf{year} + -317.1 \cdot \mathbf{sex}\\
&+ 0.1575 \cdot \mathbf{year\times{sex}} + 0.002729 \cdot \mathbf{year}^2
\end{align}\]
| year | time | sex | with_predict |
|---|---|---|---|
| 1905 | 65.80 | M | 66.81874 |
| 1908 | 65.60 | M | 65.55576 |
| 1910 | 62.80 | M | 64.74106 |
| 1912 | 61.60 | M | 63.94819 |
| 1918 | 61.40 | M | 61.70057 |
| 1920 | 60.40 | M | 60.99502 |
| 1922 | 58.60 | M | 60.31130 |
| 1924 | 57.40 | M | 59.64941 |
| 1934 | 56.80 | M | 56.66741 |
| 1935 | 56.60 | M | 56.39922 |
| 1936 | 56.40 | M | 56.13650 |
| 1944 | 55.90 | M | 54.23115 |
| 1947 | 55.80 | M | 53.60669 |
| 1948 | 55.40 | M | 53.40946 |
| 1955 | 54.80 | M | 52.18160 |
| 1957 | 54.60 | M | 51.87991 |
| 1961 | 53.60 | M | 51.34200 |
| 1964 | 52.90 | M | 50.99587 |
| 1967 | 52.60 | M | 50.69886 |
| 1968 | 52.20 | M | 50.61078 |
| 1970 | 51.90 | M | 50.45097 |
| 1972 | 51.22 | M | 50.31300 |
| 1975 | 50.59 | M | 50.14697 |
| 1976 | 49.44 | M | 50.10254 |
| 1981 | 49.36 | M | 49.96226 |
| 1985 | 49.24 | M | 49.94827 |
| 1986 | 48.74 | M | 49.95841 |
| 1988 | 48.42 | M | 49.99508 |
| 1994 | 48.21 | M | 50.23605 |
| 2000 | 48.18 | M | 50.67349 |
| 2000 | 47.84 | M | 50.67349 |
| 1908 | 95.00 | F | 82.16082 |
| 1910 | 86.60 | F | 81.03116 |
| 1911 | 84.60 | F | 80.47451 |
| 1912 | 78.80 | F | 79.92332 |
| 1915 | 76.20 | F | 78.30250 |
| 1920 | 73.60 | F | 75.71028 |
| 1923 | 72.80 | F | 74.22044 |
| 1924 | 72.20 | F | 73.73474 |
| 1926 | 70.00 | F | 72.77971 |
| 1929 | 69.40 | F | 71.38810 |
| 1930 | 68.00 | F | 70.93515 |
| 1931 | 66.60 | F | 70.48765 |
| 1933 | 66.00 | F | 69.60903 |
| 1934 | 65.40 | F | 69.17790 |
| 1936 | 64.60 | F | 68.33203 |
| 1956 | 62.00 | F | 61.07389 |
| 1958 | 61.20 | F | 60.46814 |
| 1960 | 60.20 | F | 59.88422 |
| 1962 | 59.50 | F | 59.32213 |
| 1964 | 58.90 | F | 58.78187 |
| 1972 | 58.50 | F | 56.83913 |
| 1973 | 57.54 | F | 56.62085 |
| 1974 | 56.96 | F | 56.40802 |
| 1976 | 55.65 | F | 55.99874 |
| 1978 | 55.41 | F | 55.61129 |
| 1980 | 54.79 | F | 55.24567 |
| 1986 | 54.73 | F | 54.27978 |
| 1992 | 54.48 | F | 53.51036 |
| 1994 | 54.01 | F | 53.29755 |
| 2000 | 53.77 | F | 52.79009 |
| 2004 | 53.52 | F | 52.56093 |
model <- lm(time ~ 1 + year * sex + I(year^2), data = SwimRecords)
SwimRecords_predict <- SwimRecords %>%
mutate(with_predict= predict(model, SwimRecords))
SwimRecords_predict %>%
ggplot(aes(x = year, y = time, shape = sex)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) Two common ways:
Polynomials capture “bumps” or curves in the data, and the number of these bumps depends on the degree of the polynomial. The higher the degree, the more complex the shape the polynomial can represent.
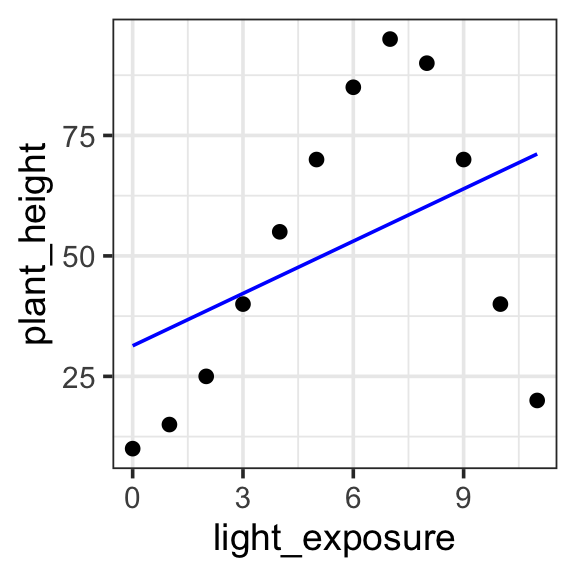
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2 \cdot \mathbf{x}\)
Call:
lm(formula = plant_height ~ 1 + light_exposure, data = poly_plants)
Coefficients:
(Intercept) light_exposure
31.346 3.619 Fitted model:
\(y = 31.346 \cdot 1 + 3.619 \cdot x\)
| plant | light_exposure | plant_height | with_formula | with_predict |
|---|---|---|---|---|
| Sunflower | 0 | 10 | 31.346 | 31.34615 |
| Sunflower | 1 | 15 | 34.965 | 34.96504 |
| Sunflower | 2 | 25 | 38.584 | 38.58392 |
| Rose | 3 | 40 | 42.203 | 42.20280 |
| Rose | 4 | 55 | 45.822 | 45.82168 |
| Rose | 5 | 70 | 49.441 | 49.44056 |
| Cactus | 6 | 85 | 53.060 | 53.05944 |
| Cactus | 7 | 95 | 56.679 | 56.67832 |
| Cactus | 8 | 90 | 60.298 | 60.29720 |
| Orchid | 9 | 70 | 63.917 | 63.91608 |
| Orchid | 10 | 40 | 67.536 | 67.53496 |
| Orchid | 11 | 20 | 71.155 | 71.15385 |
poly_plants <- read_csv('https://kschuler.github.io/datasci/assests/csv/polynomial_plants.csv')
model <- lm(plant_height ~ 1 + light_exposure, data = poly_plants)
poly_plants <- poly_plants %>%
mutate(with_formula = 31.346*1 + 3.619*light_exposure) %>%
mutate(with_predict= predict(model, poly_plants))
poly_plants %>%
ggplot(aes(x = light_exposure, y = plant_height)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) What happens if you specify the model without the intercept term in R? y ~ x instead of y ~ 1 + x?
Try it with the poly_plants data and use ‘lm()’ or ‘infer’ to fit the model you specified. What do you noticed about the weights?
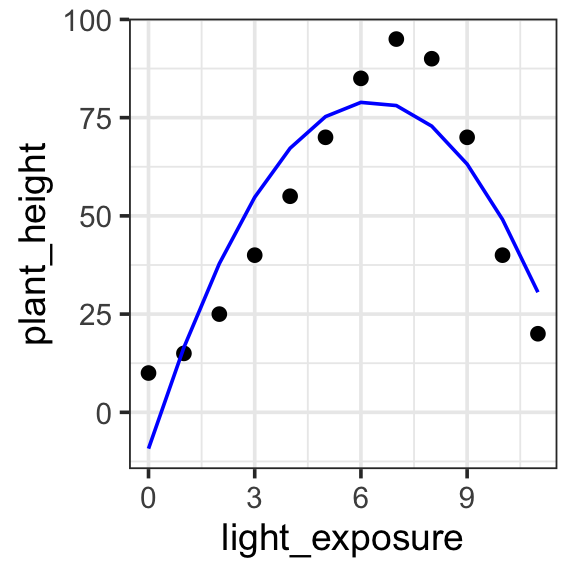
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2 \cdot \mathbf{x} + w_3 \cdot \mathbf{x}^2\)
Call:
lm(formula = plant_height ~ 1 + light_exposure + I(light_exposure^2),
data = poly_plants)
Coefficients:
(Intercept) light_exposure I(light_exposure^2)
-9.245 27.973 -2.214 Fitted model:
\(y = -9.245 \cdot\mathbf{1} + 27.973 \cdot \mathbf{x} + -2.214 \cdot \mathbf{x}^2\)
| plant | light_exposure | plant_height | with_predict |
|---|---|---|---|
| Sunflower | 0 | 10 | -9.244506 |
| Sunflower | 1 | 15 | 16.514735 |
| Sunflower | 2 | 25 | 37.845904 |
| Rose | 3 | 40 | 54.749001 |
| Rose | 4 | 55 | 67.224026 |
| Rose | 5 | 70 | 75.270979 |
| Cactus | 6 | 85 | 78.889860 |
| Cactus | 7 | 95 | 78.080669 |
| Cactus | 8 | 90 | 72.843407 |
| Orchid | 9 | 70 | 63.178072 |
| Orchid | 10 | 40 | 49.084665 |
| Orchid | 11 | 20 | 30.563187 |
model <- lm(plant_height ~ 1 + light_exposure + I(light_exposure^2), data = poly_plants)
poly_plants <- poly_plants %>%
mutate(with_predict= predict(model, poly_plants))
poly_plants %>%
ggplot(aes(x = light_exposure, y = plant_height)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) 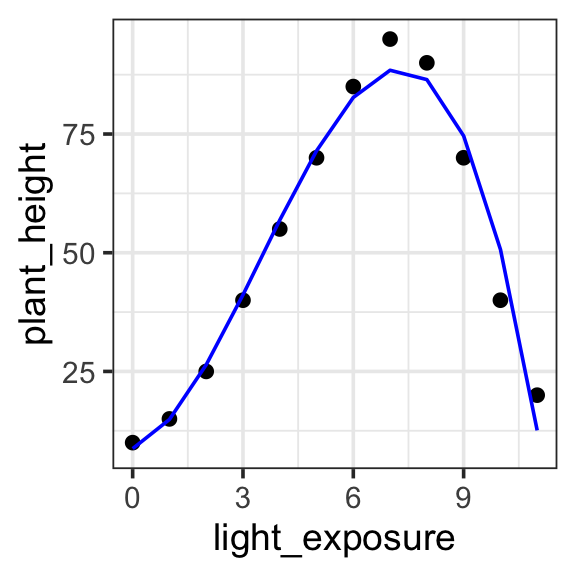
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2 \cdot \mathbf{x} + w_3 \cdot \mathbf{x}^2 + w_4 \cdot \mathbf{x}^3\)
Call:
lm(formula = plant_height ~ 1 + light_exposure + I(light_exposure^2) +
I(light_exposure^3), data = poly_plants)
Coefficients:
(Intercept) light_exposure I(light_exposure^2)
8.7363 2.7276 3.7796
I(light_exposure^3)
-0.3632 Fitted model:
\(y = 8.7363 \cdot \mathbf{1} + 2.7276 \cdot \mathbf{x} + 3.7796 \cdot \mathbf{x}^2 + -0.3632 \cdot \mathbf{x}^3\)
| plant | light_exposure | plant_height | with_predict |
|---|---|---|---|
| Sunflower | 0 | 10 | 8.736264 |
| Sunflower | 1 | 15 | 14.880120 |
| Sunflower | 2 | 25 | 26.403596 |
| Rose | 3 | 40 | 41.127206 |
| Rose | 4 | 55 | 56.871462 |
| Rose | 5 | 70 | 71.456877 |
| Cactus | 6 | 85 | 82.703963 |
| Cactus | 7 | 95 | 88.433233 |
| Cactus | 8 | 90 | 86.465202 |
| Orchid | 9 | 70 | 74.620380 |
| Orchid | 10 | 40 | 50.719281 |
| Orchid | 11 | 20 | 12.582418 |
model <- lm(plant_height ~ 1 + light_exposure + I(light_exposure^2) + I(light_exposure^3), data = poly_plants)
poly_plants <- poly_plants %>%
mutate(with_predict= predict(model, poly_plants))
poly_plants %>%
ggplot(aes(x = light_exposure, y = plant_height)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) 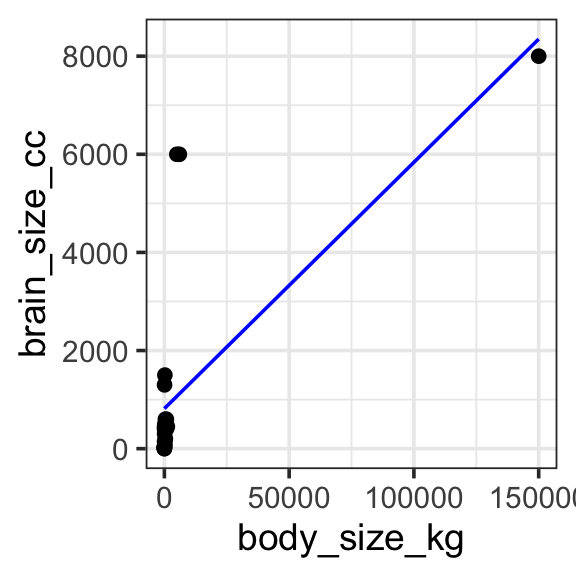
Model specification:
\(y = w_1\cdot\mathbf{1} + w_2\cdot\mathbf{body\_size\_kg}\)
Call:
lm(formula = brain_size_cc ~ 1 + body_size_kg, data = brain_data)
Coefficients:
(Intercept) body_size_kg
816.59014 0.05021 Fitted model:
\(y = 816.59014 \cdot\mathbf{1} + 0.05021 \cdot\mathbf{body\_size\_kg}\)
| Species | brain_size_cc | body_size_kg | with_predict |
|---|---|---|---|
| Mouse | 0.4 | 2.0e-02 | 816.5911 |
| Rat | 2.0 | 2.5e-01 | 816.6027 |
| Rabbit | 12.0 | 1.5e+00 | 816.6655 |
| Cat | 25.0 | 4.5e+00 | 816.8161 |
| Dog | 50.0 | 1.0e+01 | 817.0923 |
| Sheep | 150.0 | 7.0e+01 | 820.1049 |
| Pig | 300.0 | 1.0e+02 | 821.6113 |
| Goat | 450.0 | 5.0e+01 | 819.1007 |
| Gorilla | 500.0 | 1.8e+02 | 825.6282 |
| Horse | 600.0 | 4.0e+02 | 836.6747 |
| Human | 1300.0 | 7.0e+01 | 820.1049 |
| Chimpanzee | 400.0 | 6.0e+01 | 819.6028 |
| Dolphin | 1500.0 | 2.0e+02 | 826.6324 |
| Whale (Orca) | 6000.0 | 5.0e+03 | 1067.6469 |
| Elephant | 6000.0 | 6.0e+03 | 1117.8583 |
| Blue Whale | 8000.0 | 1.5e+05 | 8348.2943 |
| Giraffe | 600.0 | 8.0e+02 | 856.7592 |
| Rhinoceros | 450.0 | 1.2e+03 | 876.8438 |
| Walrus | 400.0 | 8.0e+02 | 856.7592 |
| Tiger | 90.0 | 2.2e+02 | 827.6366 |
| Kangaroo | 50.0 | 6.0e+01 | 819.6028 |
| Crocodile | 200.0 | 4.0e+02 | 836.6747 |
| Penguin | 20.0 | 3.0e+01 | 818.0965 |
brain_data <- read_csv('https://kschuler.github.io/datasci/assests/csv/animal_brain_body_size.csv') %>%
rename(brain_size_cc = `Brain Size (cc)`, body_size_kg = `Body Size (kg)`)
model <- lm(brain_size_cc ~ 1 + body_size_kg, data = brain_data)
brain_data <- brain_data %>%
mutate(with_predict= predict(model, brain_data))
brain_data %>%
ggplot(aes(x = body_size_kg, y = brain_size_cc)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14) 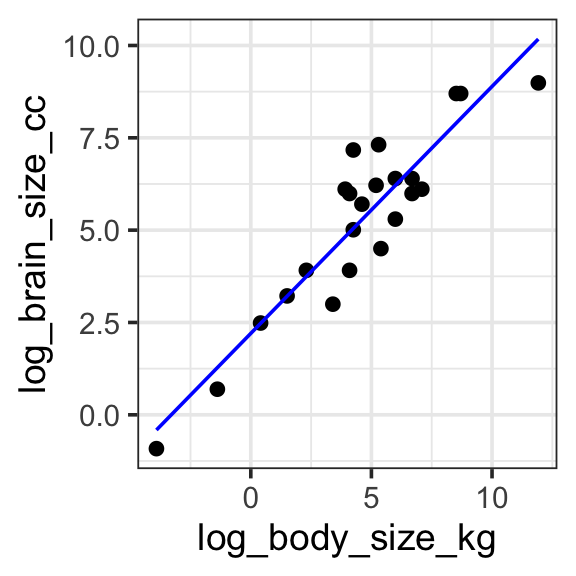
Model specification:
\(log(y) = w_1\cdot\mathbf{1} + w_2 \cdot log(\mathbf{body\_size\_kg})\)
Call:
lm(formula = log(brain_size_cc) ~ 1 + log(body_size_kg), data = brain_data)
Coefficients:
(Intercept) log(body_size_kg)
2.2042 0.6687 Fitted model:
\(log(y) = 2.2042\cdot\mathbf{1} + 0.6687 \cdot log(\mathbf{body\_size\_kg})\)
| Species | brain_size_cc | body_size_kg | log_brain_size_cc | log_body_size_kg | with_predict |
|---|---|---|---|---|---|
| Mouse | 0.4 | 2.0e-02 | -0.9162907 | -3.9120230 | -0.4116321 |
| Rat | 2.0 | 2.5e-01 | 0.6931472 | -1.3862944 | 1.2772249 |
| Rabbit | 12.0 | 1.5e+00 | 2.4849066 | 0.4054651 | 2.4753051 |
| Cat | 25.0 | 4.5e+00 | 3.2188758 | 1.5040774 | 3.2099046 |
| Dog | 50.0 | 1.0e+01 | 3.9120230 | 2.3025851 | 3.7438358 |
| Sheep | 150.0 | 7.0e+01 | 5.0106353 | 4.2484952 | 5.0449906 |
| Pig | 300.0 | 1.0e+02 | 5.7037825 | 4.6051702 | 5.2834853 |
| Goat | 450.0 | 5.0e+01 | 6.1092476 | 3.9120230 | 4.8200046 |
| Gorilla | 500.0 | 1.8e+02 | 6.2146081 | 5.1929569 | 5.6765155 |
| Horse | 600.0 | 4.0e+02 | 6.3969297 | 5.9914645 | 6.2104467 |
| Human | 1300.0 | 7.0e+01 | 7.1701195 | 4.2484952 | 5.0449906 |
| Chimpanzee | 400.0 | 6.0e+01 | 5.9914645 | 4.0943446 | 4.9419160 |
| Dolphin | 1500.0 | 2.0e+02 | 7.3132204 | 5.2983174 | 5.7469660 |
| Whale (Orca) | 6000.0 | 5.0e+03 | 8.6995147 | 8.5171932 | 7.8993037 |
| Elephant | 6000.0 | 6.0e+03 | 8.6995147 | 8.6995147 | 8.0212150 |
| Blue Whale | 8000.0 | 1.5e+05 | 8.9871968 | 11.9183906 | 10.1735527 |
| Giraffe | 600.0 | 8.0e+02 | 6.3969297 | 6.6846117 | 6.6739274 |
| Rhinoceros | 450.0 | 1.2e+03 | 6.1092476 | 7.0900768 | 6.9450462 |
| Walrus | 400.0 | 8.0e+02 | 5.9914645 | 6.6846117 | 6.6739274 |
| Tiger | 90.0 | 2.2e+02 | 4.4998097 | 5.3936275 | 5.8106962 |
| Kangaroo | 50.0 | 6.0e+01 | 3.9120230 | 4.0943446 | 4.9419160 |
| Crocodile | 200.0 | 4.0e+02 | 5.2983174 | 5.9914645 | 6.2104467 |
| Penguin | 20.0 | 3.0e+01 | 2.9957323 | 3.4011974 | 4.4784353 |
model <- lm(log(brain_size_cc) ~ 1 + log(body_size_kg), data = brain_data)
brain_data <- brain_data %>%
mutate(
log_brain_size_cc = log(brain_size_cc),
log_body_size_kg = log(body_size_kg)
) %>%
mutate(with_predict= predict(model, brain_data))
brain_data %>%
ggplot(aes(x = log_body_size_kg, y = log_brain_size_cc)) +
geom_point() +
geom_line(aes(y = with_predict), color = "blue") +
theme_bw(base_size = 14)